Проектирование реконструкции железной дороги: Методические указания к курсовому проектированию, страница 14

3.3.2. Увеличение радиуса круговой кривой

Цель задачи – определить смещения N (м) от оси существующего до оси проектного пути.

Задача решается для правильной (выправленной) круговой кривой. Положение подходных прямых сохраняется, т.е. в  существующий угол поворота вписывается круговая кривая большего радиуса.

Исходные данные:

·  радиус существующей кривой R_c (м);

·  радиус проектной кривой R_пр (м);

·  угол поворота кривой φ (перевести в радианы);

·  пикет начала существующей круговой кривой (НКК_с).

Смещения можно определять точно, как нормали в локальной системе декартовых координат, или приближенно, как эвольвенты методом угловых диаграмм. Рекомендуется использовать оба метода, чтобы сопоставить точность результатов.

Решение в локальной системе декартовых координат. Схема решения показана на рис. 3.7.

Начало координат помещено в точку О_с центра существующей кривой.  Координаты центра проектной кривой

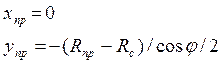
Определение смещений. Задача симметрична относительно оси Y; поэтому смещения можно рассчитывать только для одной половины, например, для левой.

Рис.3.7. Расчетная схема в локальной системе координат

На участке от НКК_пр до НКК_с  расстояния k₁ отсчитываются от НКК_пр до каждой точки деления (двадцатки), попавшей в этот промежуток. Смещения N в каждой такой точке определяются как

На участке  от НКК_с до середины кривой расстояния k₂ удобнее отсчитывать от середины существующей кривой в сторону НКК_с, т.е. справа налево (к точке m на рис. 3.7).

Угол в радианах между осью Y и прямой  О_сn  равен  γ=k₂/R_с .

Смещение оси пути (нормаль) равно      .

Для определения длины отрезка O_c n необходимо определить координаты точки n пересечения проектной кривой и прямой О_сm, для чего решить систему уравнений

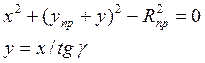
Здесь:

 первое уравнение – уравнение проектной кривой в выбранной системе координат, где всегда у_пр<0, второе - уравнение прямой O_cm.

После подстановки получим уравнение

,

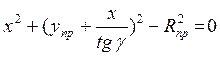которое легко решается, либо приведением к квадратному, либо с помощью MathCAD. Из двух полученных результатов  определения координаты х выбирается реальный,  подсчитывается координата у=х/tgγ и длина отрезка  О_сn       

Смещение равно   

Решение методом угловых диаграмм.  Для решения задачи вычерчиваются совмещенные угловые диаграммы существующей и проектной кривых. Осью длин при построении служит ось существующего плана (рис.3.8).

Смещение s определяется как разность площадей угловых диаграмм проектной и существующей кривых.  В первой половине, от НКК_пр до средней точки, эта разность положительна, т.к. площадь угловой диаграммы проектной кривой больше, чем площадь угловой диаграммы существующей. В средней точке (СК) смещение максимально, а потом оно уменьшается до нуля в точке ККК_пр.

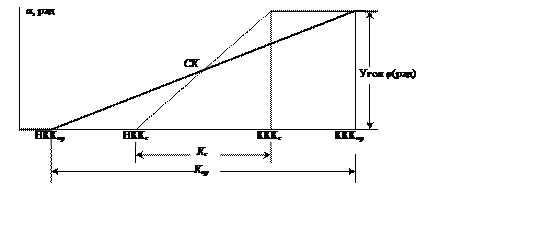
Рис.3.8. Угловые диаграммы существующей и проектной кривых

Задача симметрична, поэтому, как и в точном методе, можно ограничиться только первой половиной расчета.

Ниже приведен пример расчета точным и приближенным способами. Исходные данные примера: R_с=600 м; R_пр=1200 м; φ = 32⁰ 24' = 0,565487 рад.;  пк НКК_с=120+21,40.

Тангенсы существующей и проектной кривых

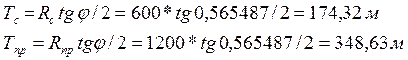
Разность тангенсов ΔТ= 348,63–174,32=174,31 м

Длины существующей и проектной кривых

K_c = R_cj = 600*0,565487 = 339,29

K_пр = R_прj = 1200*0,565487 = 678,58

Пикетаж главных точек считается от пк НКК_с:

пкНКК_пр=пкНКК_с–ΔТ=пк120+21,40–(174,31)=пк118+47,09

пкККК_с=пкНКК_с+К_с=пк120+21,40+(339,29)=пк123+60,69

пкСК=пкНКК_с+К_с/2=пк120+21,40+(339,29/2)=пк121+91,04

пкККК_пр=пкККК_с+ΔТ=пк123+60,69+(174,31)=пк125+35,00

Расчет точным методом. Смещения в интервале от НКК_пр до НКК_с удобно выполнять в Excel. Пикетное значение лучше заносить в метрах (12021,40 вместо пк 120+21,40). В табл.3.9 показано вычисление смещений на участке от НКК_пр до НКК_с.

Таблица 3.9

Расчет смещений на участке от НКК_пр до НКК_с