Проектирование реконструкции железной дороги: Методические указания к курсовому проектированию, страница 10

С – площади угловой диаграммы проектной кривой во всех точках деления в пределах круговой кривой ω₁=k₁²/2R; 

D – нули до пк ККК включительно; далее, до конца полевых замеров (точки Б), расстояния  k₂ от ККК до точек деления кривой; например,  для точки пк 251+80 k₂=(251,8000 – 251,6574)*100 = 14,26 м и т.д.;

Е – площадь угловой диаграммы проектной кривой за пкККК:

ω₂= площадь до точки ККК+ k₂*φ = 16,263+14,26*0,22544=19,478;

F – сложение значений в колонках С и Е  ω_п =ω₁+ω₂; 

G - площадь угловой диаграммы существующей кривой ω_с (импортировать соответствующую колонку из табл.3.3);

Н - сдвижка от устройства круговой кривой в м   ∆=ω_п – ω_с.

В результате получены преимущественно отрицательные сдвиги, которые можно компенсировать за счет устройства переходной кривой определенной длины.

Если отрицательные сдвиги получились слишком большими или они оказались положительными, то их можно уменьшить, вернувшись к шагу 2 и подобрав другой радиус круговой кривой.

Шаг 5. Сдвиги после устройства переходной кривой. Смещение от устройства переходной кривой длиной l в пределах «чистой» круговой (между КПК1 и КПК2) равно 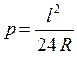 . Эти смещения всегда положительны, т.е. направлены к центру кривой. В примере получено удачное решение, когда сдвиги от круговой кривой преимущественно отрицательны, т.е. направлены от центра.

Поэтому целесообразно подобрать переходную кривую такой длины, чтобы смещение p равнялось примерно 0,40 м. При выбранном  смещении p и радиусе проектной кривой R длина переходной кривой

, м

Для условий примера при  р=0,40 м и R=640 м получена длина переходной кривой 78,38 м. Округлив этот результат до целых десятков метров  l = 80 м, получим сдвиг в пределах круговой кривой р=0,42 м.

При определении пикетов начала и концов переходных кривых с достаточной для расчета  сдвигов точностью принято считать, что начала переходных кривых НПК1 и НПК2 выходят на l/2 от НКК и ККК на прямые, а концы переходных кривых КПК1 и КПК2 заходят в кривую на l/2 от тех же точек НКК и ККК (рис. 3.5).

Пикеты точек начал и концов переходных кривых в примере:

пк НПК1=пк НКК – l/2, пк 249+81,46

пк КПК1=пк НКК + l/2, пк 250+61,46

пк НПК2=пк ККК+l/2, пк 252+05,74

пк КПК2=пк ККК-l/2, пк 251+25,74

Рис.3.5. Взаимное расположение точек начал и концов

круговой и переходных кривых

Смещение круговой кривой к центру на величину р делается в промежутке между внутренними концами переходных кривых, т.е. между КПК1 и КПК2. В пределах переходной кривой радиус непостоянен и изменяется от бесконечности в точках НПК1 и НПК2 до величины R в точках КПК1 и КПК2.  Смещение δ в характерных точках переходной кривой: в точках НПК1 и НПК2  δ = 0; в точках НКК и ККК  δ = p/2; в точках  КПК1 и КПК2  δ = р.

Для определения смещений от переходной кривой δ во всех точках деления, попавших в интервалы НПК1-КПК1 и НПК2-КПК2, находят расстояния s (м). Эти расстояния для первой переходной кривой отсчитываются от НПК1 в сторону КПК1, а для второй переходной кривой - от НПК2 в сторону КПК2.

Смещения δ определяются по формулам

при   0 < s < l/2 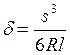          при l/2 < s < l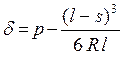    

Окончательный сдвиг равен алгебраической сумме сдвигов ∆ от круговой и δ (или р) от переходной кривой:

в пределах  переходных кривых НПК1-КПК1 и НПК2-КПК2

∆_ок = ∆ + δ;

между КПК1 и КПК2, т.е. в пределах круговой кривой  

∆_ок = ∆ + р.

Расчеты сведены в табл.3.5.

Пропущенные строки - это главные точки кривой, не совпадающие с точками её деления,  для которых не определена площадь угловой диаграммы существующей кривой.

3.2.3. Расчет комбинированным методом (вариант 2)

Шаги 1-3 выполняются одинаково с вар. 1, т.е. радиус проектной кривой известен. Отличие состоит в том, что сдвиги определяются не в виде эвольвент, как в п.3.2, а как строгие нормали.

Локальная система декартовых координат, принятая для расчета, показана на рис. 3.6. За ось х взята продленная вправо начальная прямая. Центр координат расположен в точке начала полевой съемки.  Ось у направлена в сторону поворота кривой.