Построение математических моделей исследуемых систем на основании экспериментальных данных

Введение

          При исследовании объектов для нахождения разумного решения, связанного с управлением или оптимизацией нужно составить математическую модель системы или исследуемого процесса.  

          Существуют два  пути составления такой математической модели:

          1.Аналитический.

          На  основании физики процесса, химических и прочих соотношений можно составить систему дифференциальных или алгебраических уравнений и получить исходные данные для составления модели. Этот путь реализуется редко, т.к. системы могут быть очень сложными, а связи нечетко определенными.

          2.Статистический.

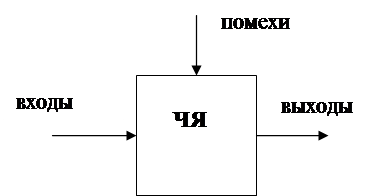          Система  представляется ”черным ящиком” с неизвестными  характеристика- ми (рис.1).

                                   рис.1

Можно подавать сигналы на входы и измерять выходные сигналы. И на основании анализа этих данных составим систему алгебраических или дифференциальных уравнений. Входные и выходные сигналы должны измеряться. Это приводит  к ошибкам. На “черный ящик” действуют помехи. И соотношения получаются в виде усредненных характеристик.

          По этой причине основным математическим аппаратом анализа является аппарат математической статистики.

          Математические модели систем обычно бывают двух типов:

          - статические:поведение   системы   исследуется   в   установившемся           режиме.

          - динамические:характеристики   системы   определяются   в   переходном режиме.

          Задачи построения модели обычно связаны с необходимостью определения структуры математической модели и ее параметров. При этом необходимо иметь возможность определить достоверность и степень достоверности полученных результатов. Основные задачи при расчете характеристик зависят от способа проведения эксперимента:

          - пассивный эксперимент:предполагает  известный набор данных, характеризующих состояния интересующего объекта.

          - активный эксперимент  (планируемый):предполагается отсутствие предварительной информации, а эксперимент проводится по специально разработанному плану.

В качестве основных задач исследования можно назвать следующие:

1)  Т.о. провести эксперименты, чтобы их число было минимальным, а точность результатов максимальной.

2)  Нужно использовать алгоритмы, которые позволяют обработать информацию т.о., чтобы получить максимальную информацию об объектах.

3)  Какие обоснованные выводы можно сделать на основании произведенных экспериментов.      

1.  ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК И ПРОВЕРКИ ГИПОТЕЗ

          1.1.Выборки и выборочные функции.

          Совокупность X₁,X₂,...,X_n    n-независимых случайных величин X_i, распределен-

ных по одному и тому же закону, совпадающему с законом распределения генеральной совокупности, называется выборкой объема  n  из генеральной совокупности X.

Совокупность х₁,х₂,...,х_n , полученная в результате  n  экспериментов называется реализацией выборки.

          Если (X₁,X₂,...,X_n) выборка, то   = j(X₁,X₂,...,X_n ) называется  выборочной функцией (оценкой). 

           =  j( х₁,х₂,...,х_n )  - реализация выборочной функции (реализация оценки).

Так, например, выборочная функция 

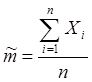              называется оценкой математического  ожидания случайной вели-

чины X.  Оценка    является в свою очередь также случайной величиной.

 ,

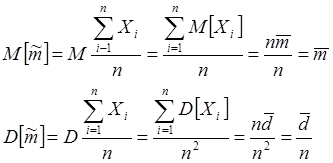где    - истинные значения математического ожидания  и дисперсии оценки  .    

          В силу центральной предельной теоремы можно полагать, что при , распределение оценки    будет приближаться к нормальному.

 

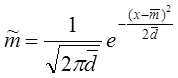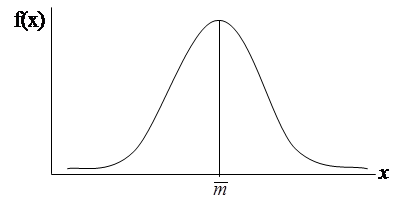
рис.2.

                   Функция плотности вероятности оценки

Выборочная функция, позволяющая рассчитать дисперсию случайной величины выглядит следующим образом :

 

          Перечисленные оценки называются точечными. Для точечных оценок обычно выдвигаются следующие требования :

              (несмещеность оценки)

             (эффективность оценки)

  (состоятельность оценки)

          Все оценки являются случайными величинами и для определения их характеристик нужно знать законы их распределения. При статистических исследованиях используются главным образом четыре вида распределения, примерный вид которых приведен на рис.3.

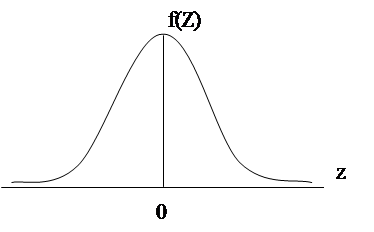
 рис.3(а).

          Нормальный закон распределения  с нулевым математическим  ожиданием и единичной дисперсией.

 

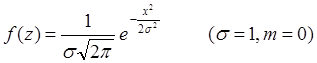
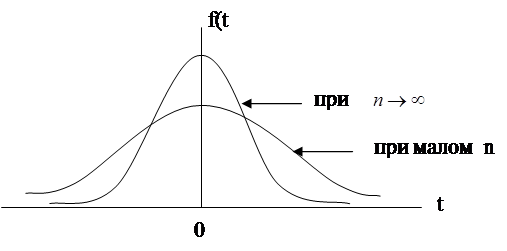
      рис.3(б).

          Распределение Стьюдента        

 

                

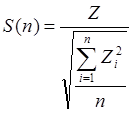рис.3(в).

          Распределение     χ²  (хи квадрат)

 

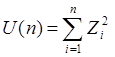
рис.3(г).

          Распределение Фишера

          n₁ – число степеней свободы числителя.

n₂ – число степеней свободы знаменателя.

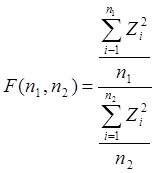
                                                  Рис. 3

Основные законы распределения используемые в статистике.

          1.2.Доверительный интервал.