Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 10

          Информационная матрица плана  Х^ТХ  будет единичной, т.е. Х^ТХ = 8 Е₈.

          Дисперсионная матрица :   (Х^ТХ)^-1 = 1/8 Е₈.

          Вектор оценок коэффициентов определяется как: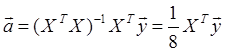   

Дальше можно определить дисперсию: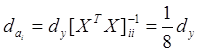 

          Регрессионная  зависимость y  от , коэффициенты которой можно рассчитать с помощью рассмотренного плана, выглядит следующим образом:

          Если зависимость имеет более простой вид: ,

то не имеет смысла производить 8 экспериментов, т.к. заведомо коэффициенты а₁₂, а_13,  а_23,  а₁₂₃ будут равны нулю.

          4.1.3.Дробные реплики полного факторного плана.

          Условная запись 2^3-1 означает “ полуреплику полного факторного эксперимента 2³ ”. Такой план и результат эксперимента может быть описан следующей таблицей:

а  регрессионная  зависимость:

Получаем  четыре уравнения с четырьмя неизвестными. Решение этой задачи аналогично решению полного факторного эксперимента 2². Для этого плана необходимо ввести новую переменную  х₃ = х₁х₂ . Это уравнение называется генерирующим соотношением.

В полном виде план эксперимента 2^3-1 и его результаты характеризуется следующей таблицей:

Этот план является полурепликой полного факторного плана. Отметим, что векторная составляющая х₂х₃  не отличается от х₁, х₁х₂ не отличается от х₃, х₂ не отличается от х₁х₃, х₀ не отличается от х₁х₂х₃. Если бы мы определяли по этому плану значения коэффициентов, мы бы не могли определить их независимо, т.е. оценки коэффициента определялись бы суммой:

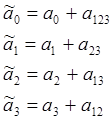          Если коэффициенты  a_ij  не точно равны нулю, то определение их по полурепликам плана ведет к погрешности (смещению оценки).

          Для определения смещения оценок используется определяющее соотношение (определяющий контраст). Так как , то при домножении генерирующего соотношения на  х₃ (слева и справа) получим:                   

 Откуда  х₁х₂х₃ = 1.

          Это соотношение называется определяющим. С его помощью просто установить  смещение коэффициентов при плане соответствующем данной полуреплике.

          Если поочередно умножать определяющее соотношение на х_i устанавливается соответствие:

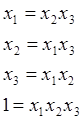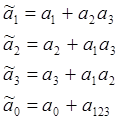          Рассмотрим полуреплику  2^5-1, позволяющую рассчитать параметры 16 коэффициентов регрессионной зависимости. Выберем генерирующее соотношение   х₅  =  х₁х₂  . Тогда определяющее соотношение имеет вид:   1 = х₁х₂х₅ .

          Матрица плана строится по вышеописанному принципу и позволяет расчитать оценки 16 параметров линейной регрессионной зависимости, если положить, например,

x₆ = x₁x₃,   x₇ = x₁x₄,   x₈ = x₂x₃,   x₉ = x₂x₄,   x₁₀ = x₃x₄,  

x₁₁ = x₁x₂x₃,   x₁₂ = x₁x₃x₄,   x₁₃ = x₂x₃x₄,   x₁₄ = x₁x₂x₄,   x₁₅ = x₁x₂x₃ x₄,