Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 16

          Запишем уравнение, соответствующее рассеянию  y  относительно общего среднего (S_G)  и выразим результат в виде суммы квадратов, связанных с рассеиванием между уровнями фактора А (S_А) и  суммы квадратов, связанных с рассеянием внутри  отдельных уровней фактора А (S_R)  или  S_G = S_A + S_R.

          Все составляющие этого уравнения  пропорциональны соответствующим дисперсиям.

          Составляющая  S_G – характеризует  полную дисперсию.

          S_А – характеризует дисперсию между  типами приборов (уровнями фактора А).

          S_R – характеризует дисперсию внутри каждого типа прибора (внутри уровня фактора А).

          Число степеней свободы составляющих дисперсии определяется в соответствии с теоремой  Кокрэна.

Теорема  Кокрэна.

          Если  i  случайных величин  имеют   распределение с  v_i  числом степеней свободы  , то сумма этих случайных величин имеет  распределение с числом степеней свободы  равным  , то есть:

          Если при расчете дисперсии  d_G и d_A надо учитывать соответственно  pn-1, и p-1   степеней свободы, то: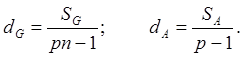    

          (pn - 1) = ( p – 1 ) + x;

Отсюда находим, что  x = p (n – 1),  таким образом при расчете дисперсии  d_R  число степеней свободы определяется как  p(n – 1):          .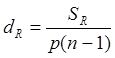

          Если дисперсии результатов измерения между различными приборами больше, чем для одного прибора (внутри данного уровня фактора А), то тогда систематические ошибки показаний приборов существенно различны.

          Для сравнения дисперсий используется отношение Фишера:  .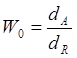      

По величине  W₀  можно судить, об одинаковости или различии этих дисперсий.  Если это отношение мало, то отличие в систематических ошибках приборов незначительно. 

          При выполнении расчета с помощью ППП (например, StatGraphics) результаты расчетов выдаются в виде следующей таблицы:

            Таблица дисперсионного анализа при однофакторной классификации.

          За основную гипотезу  Н₀  принимается гипотеза о том, что отклонения в показаниях приборов несущественно,  т.е. различие  между уровнями факторов несущественно. Следовательно, если принять уровень значимости равным  0.05 , то

          при   >  0.05  принимается  гипотеза  Н₀;

          при   <  0.05  принимается  гипотеза  Н₁.

Если  справедлива гипотеза  Н₁, то для определения отклонений в уровнях фактора А обычно рассчитываются  предельные (95% доверительный интервал) отклонения выходной величины  y  при заданном уровне фактора  А.  В ППП  StatGraphics  для наглядного представления влияния уровней фактора  А  используется график “ящик и усы” (Box and whisker plot) рис.16.

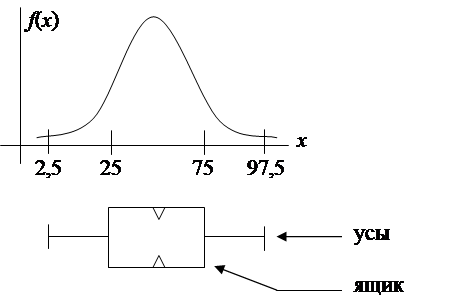
                                  рис. 16  

          График “ящик и усы” и связанный  с  этим  графиком  вид  функции

плотности  вероятности   f(x).  Выемка  в “ящике” соответствует

математическому ожиданию  М[x].

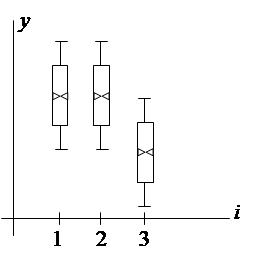          На  рис.17  демонстрируется  влияние  уровня  фактора  А  номера  прибора на результаты  y (показания  приборов). Как видно  из этого графика,  показания  (систематическая  ошибка)  третьего  прибора  существенно  отличаются  от  показаний приборов 1  и  2.

                                              рис. 17

          Влияние  i  уровня фактора  А  на значение выходной величины

          5.2.Двухфакторный  дисперсионный  анализ.

          Задача двухсторонней классификации возникает при проведении наблюдений в эксперименте, в котором одновременно действуют два фактора  А  и  В, варьируемые соответственно на  р  и  q  уровнях. Наблюдаемые  значения  у  представимы в виде: