Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 17

         

где  

Пусть, например, для определенности:

1-ый  фактор характеризует  р  типов  приборов;

2-ой  фактор характеризует  q  диапазонов температуры;

3-ий  , смешанный, фактор характеризует взаимодействие двух предыдущих.

          Условие  репараметризации:

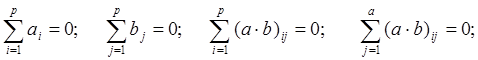
                                    при  j = 1 … q    при  i = 1 … p

          Таблица результатов измерений при  двухфакторной классификации.

i j		уровень  фактора  В
		1	2	…	q
уровень  фактора  А	1	y111 … … y11r	y121 … … y12r		y1q1 … … y1qr
	2	y211 … y21r	y221 … y22r		y2q1 … y2qr
	...	…				…
	p	yp11 … … yp1r	yp21 … … yp2r		ypq1 … … ypqr
				…

          Средние значения по строкам, по столбцам и полные средние  расчитываются по формулам:

    

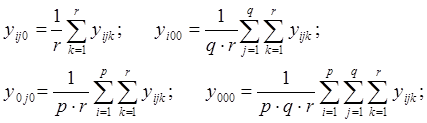
          Сумма квадратов ошибок:

    

          Если воспользоваться методом МНК, можно определить оценки значения соответствующих параметров:

    

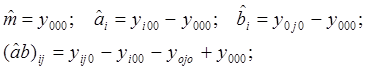
          Составим уравнения:

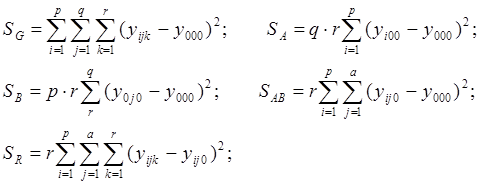
Т.о.   .

S_G   определяет  полную  дисперсию;

S_A   определяет   дисперсию по фактору  А;

S_B  определяет   дисперсию по  фактору  В;

S_AB определяют  дисперсию по взаимодействию  А  и  В;

S_R  определяет  дисперсию измерений (ошибку).

Число степеней свободы   

для 

,  следовательно  число степеней свободы х  для  S_R  определяется 

         

         Таблица дисперсионного анализа при двухфакторной классификации имеет вид:

Компоненты дисперсии	Сумма квадратов	Число       степеней      свободы	Среднеквадратичное    отклонение	Отношение Фишера	Уровень значимости
Между факторами  А	SA	p-1
Между факторами  В	SB	q-1
Между взаимодействием  АВ	SAB	(p-1)(q-1)
Ошибка (внутри    фактора)	SR	pq(r-1)
Полная	SG

          Проверяется гипотеза  Н₀

Н₀ – разница  в показаниях приборов в зависимости от типа прибора, от температуры и от их взаимодействия несущественна.

          Если 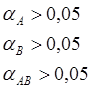     ,  то имеет  место  гипотеза  Н₀.

          Если справедлива  Н₀, то влияние факторов  А,  В  и  АВ  не существенно. Если справедлива  Н₁, то можно определить, какие из факторов оказывают существенное влияние на результат измерения  у.

5.3.Латинские  планы.

          5.3.1.Трехфакторные латинские планы.

          При использовании этих планов пренебрегают взаимным влиянием факторов.  При этих условиях можно реализовать достаточно простую модель, если предполагать, что число уровней факторов одинаково.

          Наблюдаемые значения представляются в виде:

         

где  - нормально распределенная ошибка наблюдения с нулевым математическим

                ожиданием; 

а_i, b_j, c_k – уровни фактора  А,  В,  С  при  р = 4.

          Пример экспериментального плана  при  р = 4 задается нижеследующей таблицей  (рис. 18).  В каждой строке и в каждом столбце должно быть сочетание всех уровней.

А	В	С	D
B	A	D	C
C	D	B	A
D	C	A	B

                                   рис. 18

                Четырехуровневый латинский квадрат

Первый фактор определяется строками таблицы.

Второй  фактор определяется столбцами таблицы.

Третий фактор определяется буквенным обозначением.

Если вместо буквенных обозначений ввести цифровые  (рис. 19), то результаты экспериментов, проведенных в соответствии с рассматриваемым планом можно представить таблицей 2.