С помощью определяющего соотношения можно найти смещение оценок параметров:
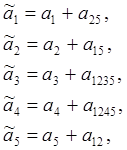 |
и т.д.
Рассмотрим четверть-реплику 25-2 для определения 6 неизвестных коэффициентов ai ( i = 0,1,…,5) с генерирующими соотношениями х4 = х1х2 и х5 = х1х2х3 . Определяющие соотношения имеют вид 1 = х1х2х4, 1 = х1х2х3х5. В результате их перемножения получим 1 = х3х4х5, обобщенное определяющее соотношение имеет вид 1 = х1х2х4 = х1х2х3х5 = х3х4х5 .
|
х0 |
х1 |
х2 |
х3 |
х4 |
х5 |
|
+ |
- |
- |
- |
+ |
- |
|
+ |
+ |
- |
- |
- |
+ |
|
+ |
- |
+ |
- |
- |
+ |
|
+ |
+ |
+ |
- |
+ |
- |
|
+ |
- |
- |
+ |
+ |
+ |
|
+ |
+ |
- |
+ |
- |
- |
|
+ |
- |
+ |
+ |
- |
- |
|
+ |
+ |
+ |
+ |
+ |
+ |
Следовательно , например,
оценка коэффициента ![]() :
:
![]()
4.1.4.Разрешающая способность дробной реплики.
Качество дробного факторного
плана характеризуется с помощью разрешающей способности плана. Разрешающая
способность плана равна наименьшему числу символов в правых частях
обобщенных определяющих соотношений. Так, например, разрешающая
способность рассмотренной выше реплики 25-2 равна трем. Это
обстоятельство условно записывается как ![]() .
.
![]() В
плане с разрешающей способностью ни
один из главных эффектов не смешивается ни с каким другим главным эффектом, но
главные эффекты хi смешаны с эффектами двухфакторных взаимодействий xixj . В
плане с разрешающей способностью IV главные эффекты хi не смешиваются
друг с другом и с эффектами 2х факторных взаимодействий.
В
плане с разрешающей способностью ни
один из главных эффектов не смешивается ни с каким другим главным эффектом, но
главные эффекты хi смешаны с эффектами двухфакторных взаимодействий xixj . В
плане с разрешающей способностью IV главные эффекты хi не смешиваются
друг с другом и с эффектами 2х факторных взаимодействий.
Проблема выбора дробных реплик является одной из основных и направлена на то, чтобы выбрать реплику, позволяющую найти несмещенную оценку всех неизвестных параметров системы.
Рассмотрим, например, регрессионную зависимость:
y = a1x1 + a2x2 + a12345 x1x2x3x4x5 .
Какую реплику следует выбрать, чтобы коэффициенты не смешивались друг с другом, т.е. не было бы искажения интересующих нас оценок параметров? Выберем дробную реплику 25-2 с генерирующим соотношением х4 = х1х2 и х5 = х1х3 , тогда определяющие соотношения 1 = х1х2х4 1 = х1х3х5 1 = х2х3х4х5 .
Обобщенное определяющее соотношение: 1 = х1х2х4 = х1х3х5 = х2х3х4х5 .
Следовательно ![]()
Генерирующие соотношения выбраны неправильно, т.к. мы получаем смещенную оценку а1 (а1 смешивается с оценкой а12345).
Выберем такую же реплику 25-2 с генерирующими соотношениями
х4 = х1х2 и х5 = х1х2х3 ,
тогда обобщенное определяющее соотношение:
1 = х1х2х4 = х1 х2х3х5 = х3х4х5 .
Находим оценки
![]() :
:
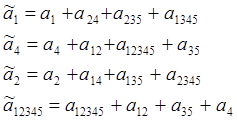
Теперь коэффициенты ![]() являются несмещенными, т.к.
являются несмещенными, т.к.
а24 = а235 = а1345 = а14 = а135 = а2345 = 0.
Коэффициент ![]() также определяется несмещенно, т.к. а4
= а12 = а35 = 0.
также определяется несмещенно, т.к. а4
= а12 = а35 = 0.
При планировании дробных факторных планов следует выбирать такие генерирующие соотношения, чтобы оценки коэффициентов регрессионной зависимости получались несмещенными.
Применение дробных реплик позволяет существенно уменьшить число экспериментов, необходимых для определения коэффициентов регрессионной зависимости.
4.1.5.Главная полуреплика.
Главной полурепликой называется реплика с максимальной разрешающей
способностью. Например, полуреплика ![]() имеет разрешающую способность IV,
имеет разрешающую способность IV,
если принять х4 = х1х2х3 , тогда определяющее соотношение имеет вид : 1 = х1х2х3х4 ;
что соответствует максимальной разрешающей способности. При этом условии
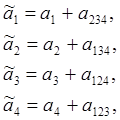
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.