Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 5

      - дисперсия случайной величины y.         

          Из приведенного соотношения следует, что  равен доле дисперсии y, “объясненной” регрессионной зависимостью:  y = j( х₁,х₂,...,х_n ).

       определяет  долю стандартного отклонения   y, оставшуюся

“необъясненной”  зависимостью от  x₁…x_к .

          Предположим, например, что   = 0,9. Тогда , откуда следует, что 44% стандартного отклонения y не объясняется зависимостью от x₁…x_к.

          Частный коэффициент корреляции.   

 определяется   как коэффициент корреляции между y и x_к при фиксированных значениях х₁,х₂,...,х_{n -1} .

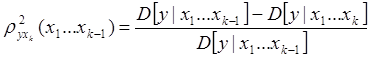
          2.4.Анализ статистической связи между ординальными (порядковыми) переменными.

К ординальным переменным относятся, как известно, переменные, позволяющие упорядочивать (ранжировать) рассматриваемые объекты по степени проявления изучаемого свойства (установить порядок, ранг объекта).

          Если обозначить   ранг  i  объекта по признаку  к , то можно определить ранговый коэффициент корреляции Спирмэна  по формуле:

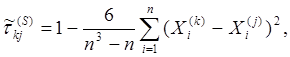 где  n- число сравниваемых рангов.

При совпадающих ранжировках   и     Если ранжировка будет противоположной (наименьший ранг  соответствует наибольшему , ). Если   , то статистическая связь между ординальными переменными отсутствует.

          Пример:

          Имеется два эксперта (к = 1, j = 2), которые должны ранжировать 10 проектов по какому-то показателю, например по экономической эффективности, зависящей от многих показателей. Результаты ранжировки этих проектов приведены ниже:

Проект	А	Б	В	Г	Д	Е	Ж	З	И	К
Оценка проекта	1	2	3	4	5	6	7	8	9	10	Эксп.1(к = 1)
	2	3	1	4	6	5	9	7	8	10	Эксп.2(j = 2)

          Для  установления  взаимосвязи  между  оценками  вычисляем  ранговый  коэффициент  корреляции:

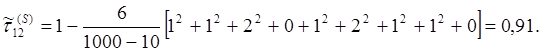
          Результат свидетельствует о достаточно точно  совпадающих оценках экспертов.

          Кроме рангового коэффициента корреляции Спирмена используется также и ранговый коэффициент корреляции Кендалла.

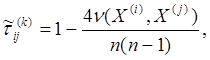
где   - минимальное число обменов соседних элементов последователь-

ности Х⁽ⁱ⁾ , необходимое для приведения ее к упорядочению Х^(j).

        при одинаковой ранжировке.

             при противоположной ранжировке

       при отсутствии статистической связи

          Рассмотрим тот же пример, связанный с экспертной оценкой 10 проектов, характеризуемой следующими данными:

Проект	А	Б	В	Г	Д	Е	Ж	З	И	К
Оценка проекта	1	2	3	4	5	6	7	8	9	10	Эксп.1
	2	3	1	4	6	5	9	7	8	10	Эксп.2

          Определяем число необходимых обмен для двух элементов 

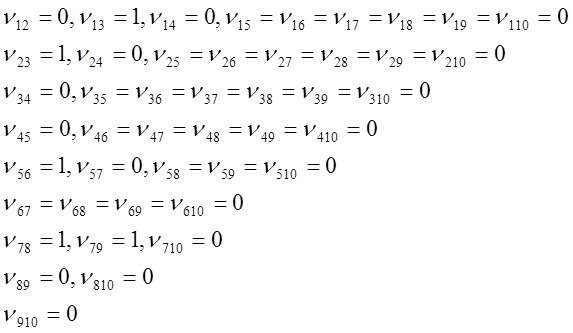
          Полное число  обмен 

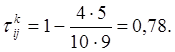
Проверка статистической значимости ранговых коэффициентов корреляции.

          Для проверки значимости коэффициента корреляции Спирмена используется следующее соотношение:

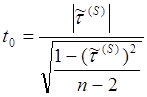
          Если  t₀ < t_0,975(n – 2), где  t_0,975(n – 2) – соответствующая процентиль распределения Стьюдента, то верна гипотеза Н₀: корреляция отсутствует.

          Для проверки значимости коэффициента корреляции Кендалла находится:

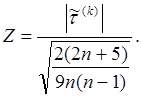
          Эта величина сравнивается с соответствующей процентилью нормального распределения  N(0,1), например Z_0,975. Если Z < Z_0,975 , то справедлива гипотеза Н₀: статистическая связь отсутствует.

          3.Исследование  вида  зависимостей  между количественными  переменными  (регрессионный  анализ).

          Рассматривается связь между некоторым числом входных (предикторных) переменных и выходной (зависимой) переменной (рис.7). X и Y – случайные величины.