Средние значения определяются по формулам:
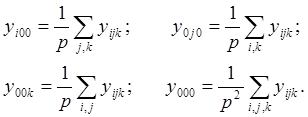
При условии репараметризации ![]() можно с помощью МНК найти оценки значений
параметров:
можно с помощью МНК найти оценки значений
параметров:
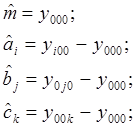
|
1 |
2 |
3 |
4 |
|
2 |
1 |
4 |
3 |
|
3 |
4 |
2 |
1 |
|
4 |
3 |
1 |
2 |
рис. 19
Четырехуровневый латинский квадрат
(с цифровыми обозначениями уровней фактора С)
Таблица 2. Результаты эксперимента.
|
i |
Уровень фактора В |
||||
|
1 |
2 |
3 |
4 |
||
|
Уровни фактора А |
1 |
у111 |
у122 |
у133 |
у144 |
|
2 |
у212 |
у221 |
у234 |
у243 |
|
|
3 |
у313 |
у324 |
у332 |
у431 |
|
|
4 |
у414 |
у423 |
у431 |
у442 |
|
Суммы квадратов отклонений находятся по формулам:
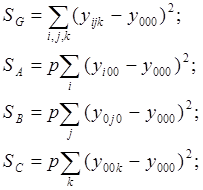
Так как ![]() ,
то сумму квадратов отклонений внутри фактора SR находим :
,
то сумму квадратов отклонений внутри фактора SR находим : ![]()
Число степеней свободы х , связанное с SR определим:
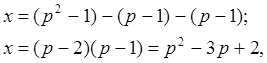
Следовательно можно определить отношение Фишера:
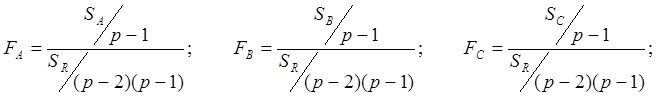
Зная отношение Фишера можно найти уровень значимости α и определить справедливость гипотезы Н0 или Н1 вышеописанным путем. Целесообразность применения латинского квадрата объясняется тем, что для решения задачи трехфакторной классификации необходимо произвести всего р2 измерений. Аналогично латинским квадратам, может быть построен латинский куб для проведения четырехфакторной классификации (рис. 20) с числом измерений равным р3.
|
1 |
2 |
3 |
4 |
|||
|
A B C D B A D C C D A B D C B A |
B A D C A B C D D C B A C D A B |
C D A B D C B A A B C D B A D C |
D C B A C D A B B A D C A B C D |
рис. 20
Слои латинского куба р = 4
5.3.2.Факторная классификация на ортогональных греко-латинских квадратах.
Используя греко-латинские квадраты можно сократить число экспериментов с р3 до р2. Два латинских квадрата называются ортогональными, если при наложении одного на другой, каждая из пар символов встречается только один раз. Чтобы построить греко-латинский квадрат, нужно использовать один латинский и один греческий квадрат (рис. 21).
|
1 |
2 |
|
|
A B C D B A D C C D A B D C B A |
α β γ δ δ γ β α β α δ γ γ δ α β |
|
Aα Bβ Cγ Dδ Bδ Aγ Dβ Cα Cβ Dα Aδ Bγ Dγ Cδ Bα Aβ |
или |
1.1 2.2 3.3 4.4 2.4 1.3 4.2 3.1 3.2 4.1 1.4 2.3 4.3 3.4 2.1 1.2 |
рис. 21
Построение греко-латинского квадрата р = 4
Результаты измерений приведены в таблице:
|
i |
Уровень фактора В |
||||
|
1 |
2 |
3 |
4 |
||
|
Уровни фактора А |
1 |
у1111 |
у1222 |
у1333 |
у1444 |
|
2 |
у2124 |
у2213 |
у2342 |
у2431 |
|
|
3 |
у3132 |
у3241 |
у3324 |
у4313 |
|
|
4 |
у4143 |
у4234 |
у4311 |
у4422 |
|
Четырехфакторная модель характеризуется следующим уравнением:
![]() ,
,
где ![]() уровни фактора A, B, C, D при р = 4,
уровни фактора A, B, C, D при р = 4,
![]() - ошибка измерения.
- ошибка измерения.
Находим суммы квадратов отклонений:
![]() с р2 – 1 степенями свободы
с р2 – 1 степенями свободы
![]()
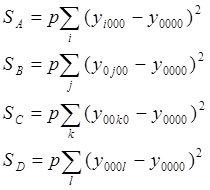 с р – 1 степенями свободы
с р – 1 степенями свободы
![]()
Число степеней свободы для SR :
![]() .
.
Определим отношение Фишера:
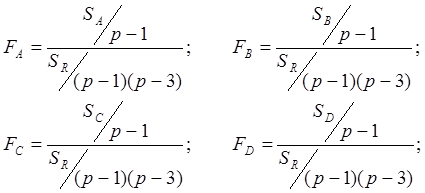
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.