Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 14

Если выбрать соответствующим образом значения α, то план Бокса может быть сделан ортогональным.

При соответствующем выборе звездных плеч план Бокса может быть сделан и рототабельным.

4.2.4.ЦКП Хартли.

Идея построения планов Хартли такая же как и у Бокса, но допускается взаимодействие парных и линейных взаимодействий.

Центральный композиционный план называется планом Хартли, если в качестве его ядра используется дробная реплика с разрешающей способностью III.

При уменьшении разрешающей способности можно уменьшить ядро плана и, следовательно, количество экспериментов N.

Недостатки плана Хартли:

1) смешение воздействий;

2) они не могут быть сделаны ни ортогональными, ни рототабельными.

Сравнение планов Бокса и Хартли.

4.2.5.Ортогональные планы Бокса.

Для определения параметров квадратичной регрессионной зависимости

можно построить ортогональный план Бокса за счет:

а) выбора величины звездного плеча;

б) видоизменения уравнения регресии путем введения дополнительных переменных:

При этом уравнение регресии принимает вид:

Коэффициент при такой замене изменится, а все остальные коэффициенты будут неизменны.

При р = 2 матрица плана имеет вид:

Аналогично строятся планы при р>2, когда ядро плана определяется ПФЭ или ДФЭ. Коэффициенты α и β определяются:

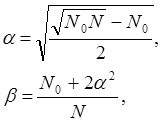где N₀ – число экспериментов, определяемое ядром плана, N – полное число экспериментов.

Если, например, N₀ = 4, то N = 9 и α = 1, β = 2/3.

Для рассматриваемого случая матрица соответствующего плана будет иметь такие параметры:

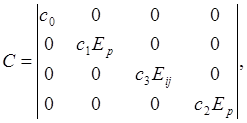Матрица этого плана получилась ортогональной, поэтому дисперсионная матрица будет диагональной.

где Е – единичная матрица.

В рассматриваемом нами примере р = 2

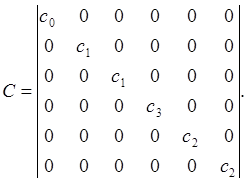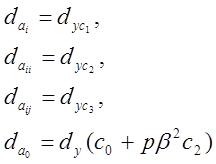Дисперсию оценок коэффициентов а можно определить следующим образом:

Для определения оценок коэффициентов a_i, a_ij, a_ii, можно использовать известное соотношение:

Истинное значение оценки коэффициентов а₀:

Расчет доверительного интервала для оценок а осуществляется с использованием статистики Стьюдента (число степеней свободы равно 1).

Для определения коэффициентов α и β используется таблица: