Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 9

          У  D-оптимального плана - минимальный объем эллипсоида рассеивания оценок  коэффициентов  а_i.

          9) План X называется G – оптимальным , если достигается наименьшая величина максимальной дисперсии оценки зависимой переменной  y  в области Ώ.

          4.1.Полные факторные планы и их дробные реплики.

          В отличие от классического эксперимента, когда факторы меняются по одному, при планировании эксперимента уровни факторов комбинируются, что позволяет уменьшить дисперсию ошибки.

          Рассмотрим, например, эксперимент, связанный с определением веса трех предметов (а₁,а₂,а₃), взвешиваемых на пружинных весах с чашей, имеющей собственный вес а₀. Тогда классический план взвешивания строится по нижеприведенной схеме, где знак “+” означает наличие груза на весах, а знак “-” отсутствие его на чашке.  y – определяет показания весов.

         

 

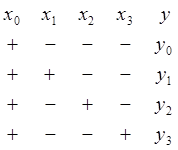
Тогда: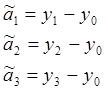  

          Дисперсия оценки веса при взвешивании предметов класическим образом равна:   , где  - дисперсия переменной y_i.

          При взвешивании путем планирования эксперимента используется матрица плана Х_n , в соответствие с которой взвешивают одновременно ряд грузов. При таком проведении эксперимента оценки     расчитываются с помощью таблицы:

 

 

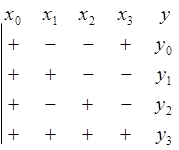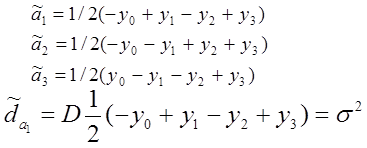Т.е. дисперсия оценки веса предметов при том же числе экспериментов оказалась в два раза меньше.

          Обычно планируются эксперименты со следующей регрессионной моделью:

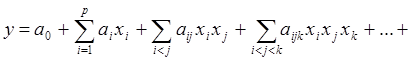
          Частный случай представляется линейной моделью 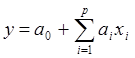 или неполной квадратичной моделью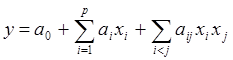  

          Факторный план называется полным, если измерения проводятся по одному для каждой возможной комбинации уровней плана.

          Если число уровней плана одинаково и равно S, то число измерений равно S^m.

Наиболее часто  S = 2 и эти уровни обозначаются  “+1” и  “-1” или просто  “+” и “-“.

          4.1.1.Полный факторный эксперимент  2².       

          При  таком  плане  производится  четыре  эксперимента. Модель  будет  выглядеть:                   

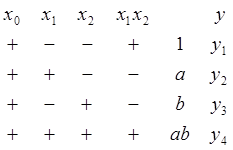а матрица плана  Х и результаты эксперимента  y:

                                                                                код

 

          Расчитаем основные характеристики модели при использовании этого плана:

 

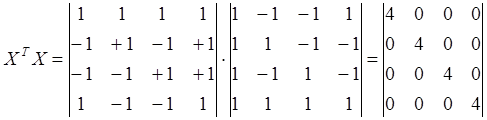          Информационная матрица  диагональна, следовательно дисперсионная матрица тоже диагональна и имеет вид:

 

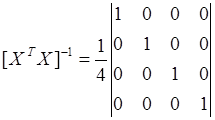          Следовательно, рассматриваемый план является одновременно и ортогональным и рототабельным.

          Рассчитаем оценку коэффициентов:   

 

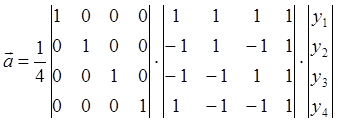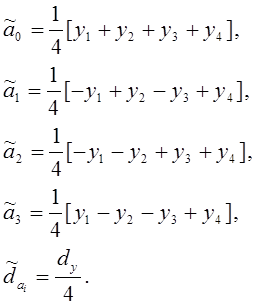откуда находим:

          Область планирования эксперимента представляет собой квадрат (рис.12). Рассматриваемый план является центральным.

 

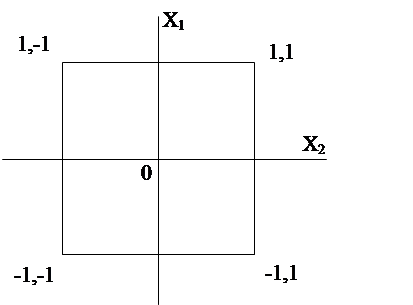                                                     рис.12            

               Область планирования полного факторного эксперимента  2².

4.1.2. Факторный план 2³.

          Для составления плана введем соответствующие переменные: х₀, х₁, х_2, х₃.

Код  “a” означает изменение знака переменной  х₁ (по сравнению с кодом 1). Код “b” означает  изменение  знака переменной х₂ , код  ab - изменение знака переменных  х₁ и х₂ .

x 0	x 1	x 2	x 3	x 1x2	x 1x3	x 2x3	x 1x2x3	код	y
+	-	-	-	+	+	+	-	1	y 1
+	+	-	-	-	-	+	+	a	y 2
+	-	+	-	-	+	-	+	b	y 3
+	+	+	-	+	-	-	-	ab	y 4
+	-	-	+	+	-	-	+	c	y 5
+	+	-	+	-	+	-	-	ac	y 6
+	-	+	+	-	-	+	-	bc	y 7
+	+	+	+	+	+	+	+	abc	y 8