Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 7

          Для того, чтобы воспользоваться методом наименьших квадратов, нужно минимизировать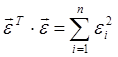

          Обозначим   ,  тогда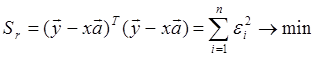  

          Для минимизации 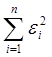  необходимо, чтобы  .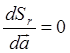

Продифференцируем по   : 

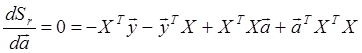
Это уравнение распадается на два, т.е. одно уравнение получается из другого путем транспонирования:

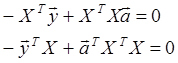
        , откуда   - уравнение, определяющее значение коэффициентов а.

                                               

          Так как  S_r – среднеквадратичное отклонение  e   , то оценка дисперсии     

ошибки   e   :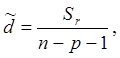  

где р – число переменных  x, n – число экспериментов.

          Отклонение  коэффициента  а_i , определяющее доверительный интервал оценок а_i  имеет распределение Стьюдента и находится по формуле:

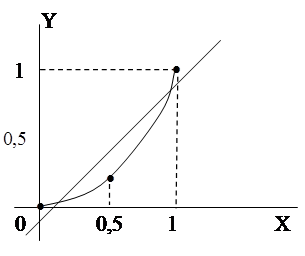Пример:   Рассмотрим  зависимость  y(x) = x²  и  найдем  наилучшую  линейную    аппроксимацию этой зависимости  y = a₀ + a₁x  (рис.9)

                                                                     

                    

            рис.9   

Зависимостьy = x ² и ее линейная аппроксимация.

 

Пусть    задается в трех точках   x ₁ = 0, x ₂ = 0.5,  x ₃ = 1, тогда векторы       и

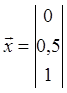
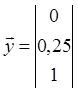имеют вид:

          Составим матрицу плана:

 

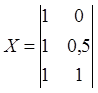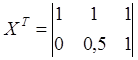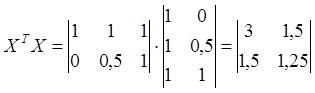          Матрица X ^ТX будет выглядеть следующим образом:

 

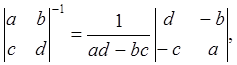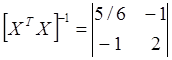          Так как                                                находим 

 

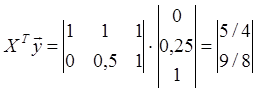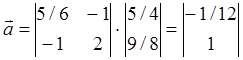          Следовательно  коэффициент  а₀ = -1/12 , коэффициент  а₁ = 1.  Т.о. аппроксимирующая линия описывается уравнением  y(x) = -1/12 + x (рис.9).

Пример2:   Пусть регрессионная зависимость имеет вид:  e

Измерения  y проводятся в шести точках:

x ₁ = -1,  x ₂ = -0.6,  x ₃ = -0.2,  x ₄ = 0.2,  x ₅ = 0.6,  x ₆ = 1.

          Точные значения  y  принимают тогда значения:

y ₁ = -1,  y ₂ = -0.2,  y ₃ = 0.6,  y ₄ = 1.4,  y ₅ = 2.2,  y ₆ = 3.

          Допустим, что ошибка  e  имеет нормальное распределение с единичной дисперсией. Если для определения  e_i  воспользоваться таблицей случайных чисел, то результаты измерений могут иметь следующий вид:

y ₁ = -1.49,  y ₂ = 1.48,  y ₃ = 0.54,  y ₄ = 0.17,  y ₅ = 1.71,  y ₆ = 3.86

 

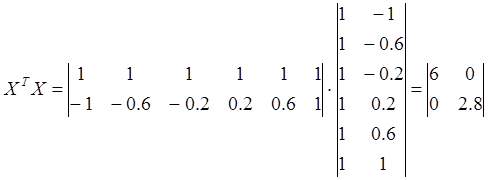          Находим   X ^ТX:

 

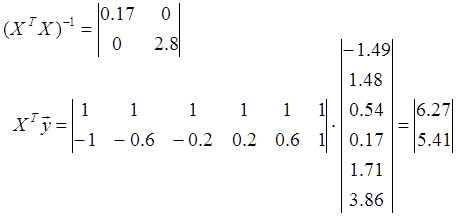
          Определяем    

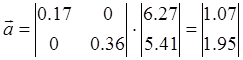
Следовательно    = 1.07        = 1.95

          Определяем доверительный интервал для  а₀ и а₁ . Для этого нужно найти оценку дисперсии   .  Для этого найдем:

 

 

                                                

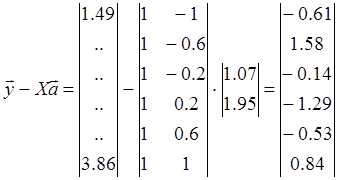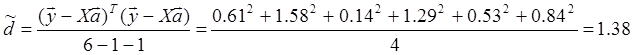          Так как  t_0,975(4) = 2.77, то

          Отклонения    велики, т.к. число экспериментов мало. Чтобы этого избежать существует два пути:

1)  увеличивать число экспериментов

2)  производят некоторое число повторных экспериментов в каждой из экспериментальных точек  x_i .

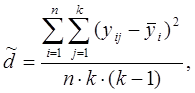Если в каждой из nточек производится к – повторных экспериментов, то оценка дисперсии вычисляется по формуле:

где     к – число повторных экспериментов в каждой из  n  точек

          y_ij – результаты  nk  измерений;

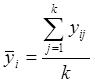 - среднее значение y;  в каждой из n точек (   ).

          Отклонения   оценок коэффициента   определяется аналогично вышеприведенному, с тем отличием, что число степеней свободы распределения Стьюдента должно равняться   т.е. :

Расчет остальных параметров регрессионной зависимости производится по вышеприведенной формуле с заменой  .

          3.3.Модель нелинейной регрессии. 

          Уравнение регрессионной зависимости имеет вид:

e_i

          Определение коэффициента а_i может осуществляться по традиционному пути, если составить матрицу плана в виде:

 

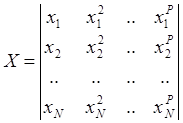          Тогда оценка вектора параметров     имеет известный вид:   

Все остальные характеристики определяются аналогично приведенным выше расчетам. Необходимо, конечно, иметь ввиду, что число экспериментов n должно быть увеличено. Так, например, для проведения параболы нужно как минимум  три точки.