Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 3

          Если проверяется альтернативная гипотеза  Н₁ :  , то она, очевидно, справедлива, если Z₀ > Z_0,975   или    >  Z_0,975 (при отрицательных значениях Z₀).

        1.3.2.Проверка гипотезы о математическом ожидании случайной величины.

          Так как отклонение этой оценки    -   m₀  распределено по закону Стьюдента, то при     >  m^­₀  выдвигают гипотезы:

          Н₀: m = m₀ (справедливо  при t₀  <  t_0,95 (n-1))

          H_1:  m > m₀ ( справедливо при t₀  >  t_0,95 (n-1)),

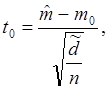где

  

t_0,95 (n-1) – 95   процентиль   распределения Стьюдента  при  (n-1)  степенях свободы, n – число экспериментов.

          При      <   m₀ , аналогично

          Н₀: m = m₀ (справедливо  при    <  t_0,95 (n-1))

          H_1:  m > m₀ ( справедливо при    >  t_0,95 (n-1)).

          Проверка альтернативной гипотезы   Н₁:   подтверждается, если

t₀ > t_0,975(n-1)  или    >  t_0,975(n-1) при отрицательных значениях  t₀.

          1.3.3.Проверка гипотезы о дисперсии случайной величины.

          Аналогично предыдущему осуществляется эта проверка с тем, однако, отличием, что в этом случае критическая область квазисимметрична (рис.4.б), так как распределение дисперсии связано с распределением χ².

          Н₀: d = d₀ при,  

          H₁: d > d₀ при    ,

          H₁: d < d₀ при     ,

при проверке односторонней гипотезы, где:

 

                                  ,

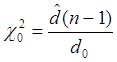       и    соответствующие процентили распределения  χ² с (n – 1) степенями свободы.

          Проверка альтернативной гипотезы  Н₁:     подтверждается, если

             или .

          1.3.4.Проверка гипотез о том, что две выборки получены из одной генеральной совокупности.

          Если при проведении двух серий экспериментов, результаты которых имеют вид:

           -  для первой серии

            -  для второй серии, где n₁,n₂ – число экспериментов серии, то для проверки гипотезы

          Н₀: m₁ = m₂       H₁:

используется оценка

 

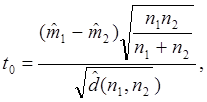где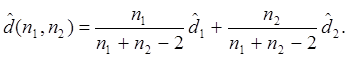 

          Гипотеза Н₀ справедлива,  если    <  t_0,95 (n₁+n₂-2), а альтернативная гипотеза Н₁ справедлива при  > t_0,95 (n₁+n₂-2), где  t_0,95(n₁+n₂-2) – 95 процентиль распределения Стьюдента с (n₁+n₂-2) степенями свободы.

          Равенство дисперсий проверяется :

          Н₀: d₁ = d₂ справедлива при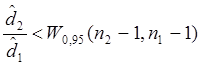

          H₁:   справедлива при  ,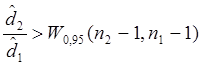

где    - 95 процентиль распределения Фишера с (n₂ – 1) числом степеней свободы числителя и (n₁ – 1) числом степеней свободы знаменателя (необходимо, чтобы   ).

          2.Основы корреляционного анализа.

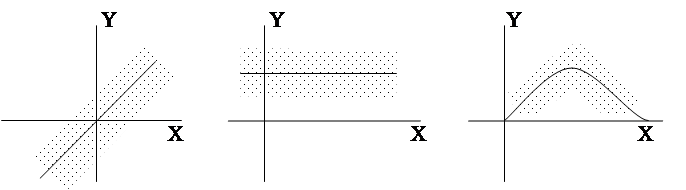
          Цель корреляционного анализа заключается в установлении факта наличия или отсутствия связи между рядом случайных величин. Связь между двумя случайными величинами  X  и  Y  может характеризоваться следующими графиками (рис.5)

         

 

                                  а)                                б)                                        в) 

                                                  рис.5.

          Результаты экспериментов, устанавливающую связь между случайными величинами Х и Y. Сплошными линиями показаны линии регресии.

         

          а) линейная связь

          б) отсутствие статистической связи

          в) нелинейная связь

          Приведенные на рис.5 графики характеризуют связь между так называемыми числовыми переменными. При корреляционном анализе необходимо также уметь находить связь между ординальными и номинальными величинами.

          Переменные x и y представляет собой  числовые переменные,  если в результате каждого эксперимента получается конкретное число, которое можно наносить на график.

          Ординальные переменные – переменные, в соответствие которым могут быть поставлены каким-то условным образом определенные числа, характеризующие степень проявления изучаемого свойства. Так, например, оценки 2,3,4,5 характеризуют степень усвоения студентом  учебного материала.