Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 12

т.е. ни один из главных коэффициентов не смешивается с коэффициентами второго порядка. Однако в частных случаях может оказаться целесообразным использование полуреплик с меньшей разрешающей способностью. Например, если регрессионная зависимость имеет вид :   

          Определим смешение коэффициентов, если  х₄ = х₁х₂х₃  и  1 = х₁х₂х₃х₄ , тогда:

 

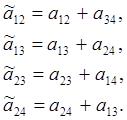          Выбор полуреплики неудачен,  т.к.  все  оценки  a_ij  смешанные.

          Выберем для этого же случая полуреплику   с генерирующим соотношением   х₄ = х₁х₂ ,  тогда  1 = х₁х₂х₄, 

 

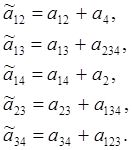
          Т.к. заведомо известно, что коэффициенты первого порядка равны нулю, то при использовании такой полуреплики получим несмещенные оценки параметров  а_ij.

          4.1.6.Факторные эксперименты с повторными наблюдениями.

          Если при каждом наборе  x_i  проводить  к  измерений, то план и результаты эксперимента можно охарактеризовать следующей таблицей:

х0	х1	х2	y
+	-	-	y11	y12	…	y1k
+	+	-	y21	y22	…	y2k
+	-	+	y31	y32	…	y3k
+	+	+	y41	y42	…	y4k

где  - среднее значение, используемое для расчета коэффициентов регрессионной зависимости по известным формулам: 

          Т.к. матрица плана ортогональная, то  (X^ТX) = 4Е      (X^ТX)^-1 = ¼ Е

 

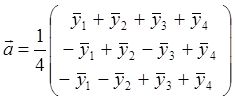          Рассмотрим определение адекватности регрессионной модели:

                    В каждой точке производится  к  экспериментов.

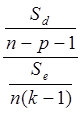                             сравнивается  с  W_0,95 [n – p – 1, n ( k – 1 )] ,

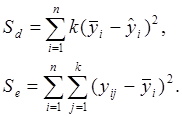где  р – число переменных  x_i (i = 1, 2, …, p)

          4.2.Планирование экстремального эксперимента.

          При проведении экстремального эксперимента необходимо найти такие значения переменных  x_i , при которых достигается экстремум некоторой функции от этих переменных ƒ(x_i). При планировании такого эксперимента удается снизить число экспериментов и повысить точность результатов. Рассмотрим, например, возможные способы поиска экстремума функций от двух переменных (рис.13).

           

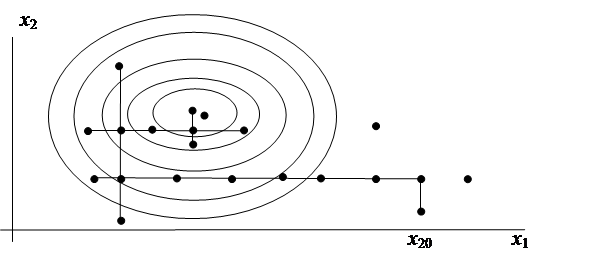
                              а) поиск экстремума при классическом  эксперименте

                                      

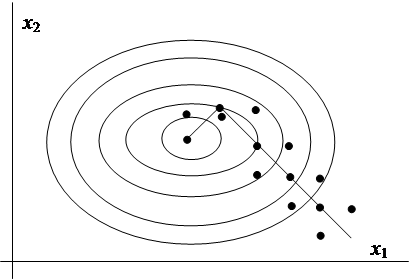
                              б) поиск экстремума при планируемом эксперименте

                                            рис. 13

          При проведении классического эксперимента поочередно меняются значения соответствующих  координат,  когда  при  изменении  первой  из  координат значение 

ƒ(х₁х₂)  начнет уменьшаться (рис.13а).

          При планируемом эксперименте производится измерение градиента ƒ(х₁х₂)  и одновременно изменяют значения  как  х₁, так и х₂ (рис.13б).

          При небольшом числе переменных  х_i  разница между методами невелика, а при большом числе переменных второй метод существенно лучше.

          4.2.1.Планирование экстремального эксперимента на участке роста (уменьшения) функции.

          Рассмотрим функцию  к  переменных  x_i  в точке  m:

 

где  вектор  .

          Чтобы осуществить движение в направлении скорейшего возрастания (убывания) функции, следует перемещаться в направлении градиента соответствующей функции:    

          Градиент определяет направление наиболее быстрого возрастания (убывания) функции.

         

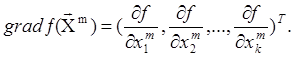
Функция от векторной переменной      может быть аппроксимирована рядом Тэйлора.

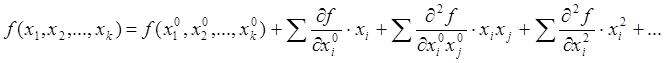
Аналогично можно представить регрессионную зависимость  от нескольких переменных

         

          Если приращения переменных  x_i  небольшие, то при аппроксимации можно отбросить квадратичные члены, и члены более высокого порядка. Рассмотрим, например, функцию от двух переменных х₁ и х₂ . Неполная квадратичная модель такой функции может анализироватьзя с помощью вышеизложенных методов планирования регрессионного эксперимента с помощью матрицы плана Х.