Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 19

          Зная отношение  Фишера  можно определить  уровень  значимости  α  и  проверить справедливость  гипотез  Н₀  или  Н₁. Следует отметить, что не все греко-латинские  квадраты  можно построить. Например,  квадраты   и   невозможно  реализовать.

          Ограничения, связанные с латинскими планами:

1)  не учитываются межфакторные взаимодействия;

2)  число уровней  р  у  всех  факторов  одинаково.

          6. СТАТИСТИЧЕСКИЙ  АНАЛИЗ  АВТОРЕГРЕССИОННЫХ 

ДИНАМИЧЕСКИХ  ЗАВИСИМОСТЕЙ.

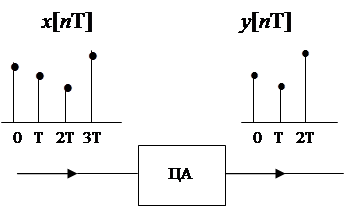
          Связь  между  входом  и выходом  динамической системы,  если входной сигнал – функция, заданная  в определенные моменты времени (решетчатый  сигнал)  определяется алгоритмом преобразования  сигнала  ЦА (рис. 22). Если использовать дискретные преобразования  Лапласа для нахождения изображения  решетчатых функций.

                                            рис. 22

          Преобразование входного сигнала  x[nT]  в  выходной  y[nT].

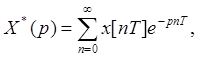
или при замене переменной  

         

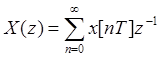
Изображение выходного сигнала определяется аналогично.

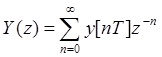
Если представить передаточную функцию дискретной системы в виде:

           

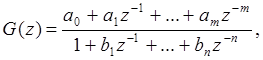
то  связь между входными и выходными сигналами дискретной системы (в области изображений) имеет вид:

         

Из  этого уравнения  получим 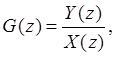  или          

Переходим к выражению, записанному в оригиналах, учитывая, что:

           

В соответствии с теоремой запаздывания :

         

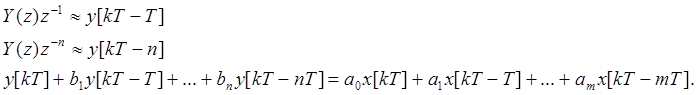
Откуда

         

          Если знать значение   х[kT]  в настоящий и предыдущие моменты времени  и  у в предыдущие моменты  времени, то можно определить  у[kT]  в настоящий момент времени. Т.е. полученное выражение представляет собой алгоритм, по которому можно определить  y[kT]  в любой момент времени.

          Рассмотрим  новую систему (рис. 23):

 

                                       

                                     рис. 23

          Системы  G(z) со случайным входным сигналом  (z).

По аналогии с рассмотренным выше примером находим:

 

Если  G(z) имеет  вид:

         

Предположим, что   - независимые случайные величины с нормальным законом распределения и дисперсии, равной  σ². Т.е.:

         

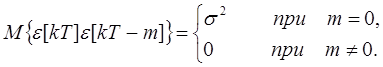
 Тогда  

          Это уравнение является уравнением регрессии. Выходная переменная  х[kT]  в  к – ый  момент времени зависит от значений этой же переменной в предыдущие моменты времени. Это уравнение определяет так называемую модель авторегрессии. Если предположим, что все b_i = 0, тогда

         

Это уравнение определяет так называемую модель скользящего среднего. Если уравнение содержит  все  a_i  и  b_i , то она определяет модель авторегрессии  и скользящего среднего. Рассмотрим модель авторегрессии  первого порядка, которая задается передаточной функцией.

         

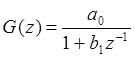
Во временной области для этой модели можно получить следующее уравнение:            

Если обозначить   то получим  :     

         

Меняя значения  к = 1, 2, …, п,  получим:

           

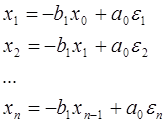
          Для решения этой системы уравнений можно применить метод наименьших квадратов, минимизируя величину 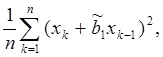 тогда:

         

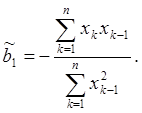
          Таким образом, если на вход системы поступает случайный сигнал с заданными характеристиками,  и на выходе снимаются данные, то можно определить  b₁ и узнать, по какому алгоритму осуществляется преобразование входного сигнала в рассматриваемой системе.  Аналогично могут быть решены задачи, связанные с определением коэффициентов  a_i  и  b_i  в более сложных случаях.

          При помощи авторегрессионного метода можно решать следующие задачи:

1)  Определение неизвестных параметров динамической системы (аналогично выше          приведенному примеру). 

2)  Прогнозирование временных рядов. Т.е. прогнозировать будущие значения выходной переменной, в том числе и доверительный интервал для этих значений, на основании анализа предыдущих значений этой переменной.

3)  Задачи, связанные с моделированием случайных временных рядов с заданными статистическими характеристиками при имитационном моделировании случайных процессов.