|
размер- ность |
ядро плана |
N |
α |
β |
элементы матрицы С |
|||
|
с0 |
с1 |
с2 |
с3 |
|||||
|
2 3 4 5 |
22 23 24 25-1 |
9 15 25 27 |
1 1.22 1.41 1.55 |
0.67 0.73 0.8 0.77 |
0.11 0.067 0.04 0.048 |
0.17 0.09 0.05 0.048 |
0.5 0.23 0.125 0.087 |
0.25 0.125 0.0625 0.0625 |
4.2.6.Рототабельные планы Бокса.
При исседовании области экстремума часто наибольший интерес представляет оценивание самой функции у, а не коэффициентов ai. Может оказаться, что в точках, одинаково удаленных от центра плана, дисперсия этих оценок будет существенно различной. Это обстоятельство вызывает определенные затруднения при исследовании области экстремума. Рототабельные планы не имеют этого недостатка. План называют рототабельным, если оценка функции отклика у в точке (х1,х2,…,хр)Т зависит лишь от расстояния этой точки от центра плана и не зависит от ее положения на гипосфере. ЦКП Бокса можно сделать рототабельным за счет выбора величины звездного плеча α и n0 кратного повторения опыта в центре плана.
Например, при р = 2 матрица рототабельного ЦКП Бокса имеет вид:
|
размер |
ядро плана |
числозв.точек |
n0 |
N |
α |
|
2 3 4 5 |
22 23 24 25-1 |
4 6 8 10 |
5 6 7 6 |
13 20 31 32 |
1.41 1.68 2 2 |
Отличие рототабельного плана от ортогонального заключается в том, что расчет дисперсии оценок коэффициентов более громоздкий, т.к. дисперсионная матрица С=(ХТХ)-1 не диагональна.
5.ДИСПЕРСИОННЫЙ АНАЛИЗ.
Часто при построении моделей систем сталкиваемся с тем, что число переменных (факторов), влияющих на выходную величину велико.
Возникает необходимость выявления переменных, играющих доминирующую роль и отсеивании всех остальных (рис.15).
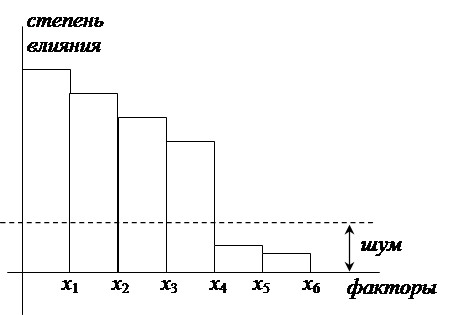
рис.15
Распределение факторов по степени их влияния на выходную величину.
Входные переменные часто оказываются номинальными или ординальными, и планы нужно строить и для этого случая.
Основная задача дисперсионного анализа заключается в анализе влияния номинальных и ординальных переменных на выходную величину и в нахождении доминирующих переменных (отсеивании несущественных переменных).
5.1.Однофакторный дисперсионный анализ.
![]() ,
,
где ![]() - ошибка наблюдения,
нормально распределенная случайная величина с мате-
- ошибка наблюдения,
нормально распределенная случайная величина с мате-
матическим ожиданием равным нулю,
m – среднее значение выходной величины,
ai – характеризует эффекты i – го уровня фактора А.
Для однозначного получения оценок параметров необходимо ввести условие репараметризации:

иначе величина m будет определяться произвольно.
Если, например, в результате эксперимента необходимо определить одинаковы ли систематические ошибки группы измерительных приборов (номер прибора определяет уровень фактора А). Результаты экспериментов удобно представлять в таблице 1.
На основании этой таблицы можно рассчитать значение переменной m и ai с помощью
метода наименьших квадратов (МНК), связанного с минимизацией суммы квадратов
ошибок: 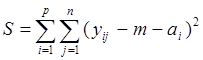
при условии 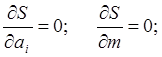
Таблица 1. Результаты эксперимента.
|
j i |
Номер наблюдения |
Сумма резуль- татов наблюдений |
Среднее |
|
|
уровень фактора А |
1 |
y11, y12, …, y1n |
|
|
|
2 |
y21, y22, …, y2n |
|
|
|
|
… |
… |
… |
… |
|
|
р |
yp1, yp2, …, ypn |
|
|
|
|
|
|
|||
Получим систему нормальных уравнений, позволяющих найти оценки параметров (при условии репараметризации):
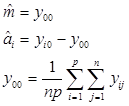
где - 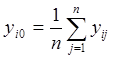 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.