Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 8

Поэтому,если уравнение модели имеет вид:  e_i,  вектор   может принимать значения   (-1, 0, 1), тогда соответствующая матрица плана будет иметь вид:   .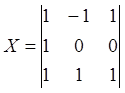

3.4.Проверка гипотезы об адекватности регрессионной модели.

          Если проверить гипотезу Н₀ о том, что рассматриваемая модель адекватна объекту, то для проверки этой гипотезы необходимо сопоставить достигнутую точность модели с величиной, характеризующей точность наблюдений. Если ошибки, характеризующие точность модели, превосходят точность наблюдений, то гипотеза Н₀ отклоняется. Поэтому, для проверки адекватности, при проведении экспериментов необходимо в каждой точке проводить несколько экспериментов с одним значением величины  i = 1,2,…, n , тогда среднее значение выходной величины

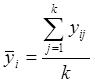
          Находим :   ,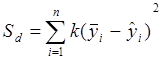

где  - расчетное значение  ,  а затем вычисляется:

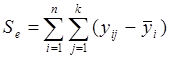
          Сравнение дисперсий находим по формуле: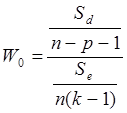 

          Если W₀ < W_0,95[n – p - 1, n(k – 1)], то принимается гипотеза Н₀. Иначе она отвергается.

                                                                     

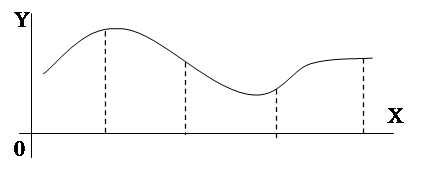
рис.10         

 Сложная регрессионная зависимость

          Если регрессионная зависимость имеет сложный характер, то подобрать подходящий полином практически не удается. Поэтому используется кусочно-параметрическая аппроксимация :

          ось Х разбивается на несколько участков, в которых выбираем линейную или квадратичную аппроксимации, наилучшим образом описывающую этот участок. Часто для этих целей используется сплайновая аппроксимация.

 4.Планирование   эксперимента  при   регрессион-

 ном анализе.

          Планирование эксперимента (активный эксперимент) позволяет:

1) повысить точность результата;

2) уменьшить число экспериментов и, следовательно, затраты на их проведение.

          Планирование эксперимента используется:

1)  для оценивания параметров регрессионных моделей;

2)  для анализа нелинейных регрессионных моделей;     

3)  планирование экстремального эксперимента;

4)  планирование эксперимента по проверке гипотез:

а) дискриминирующих экспериментов, позволяющую из ряда моделей выбрать наилучшую;

б) планирование отсеивающих экспериментов для выявления основных факторов, влияющих на результаты эксперимента;

5) планирование имитационного эксперимента, на основании которого можно построить ту или иную математическую модель рассматриваемой системы.

          Основные понятия, связанные с планированием эксперимента.

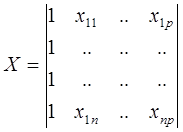Если задана матрица плана   Х, то точка 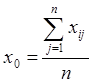         называется центром плана (рис.11).

                             

                                                                                 

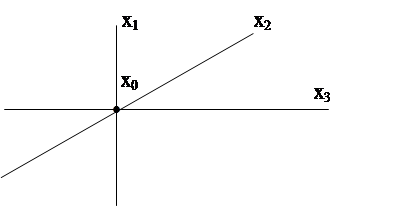
Рис.11

                               Центр плана эксперимента  x₀      

          1) План называется центральным, если  x₀ = 0;

          2) Область возможных значений входных переменных называется областью планирования экспериментов  Ώ.

          Переменные x _i называются варьируемыми переменными или факторами.  

          Если при планировании эксперимента  все   то область планирования называется гиперкубом.

          3) Матрица   Х^ТХ   называется   информационной    матрицей    плана.  Матрица [Х ^TХ]^-1  называется дисперсионной матрицей плана.

          4) План Х называется ортогональным, если информационная матрица, а, следовательно, и дисперсионная матрица, являются диагональными.

          5) План x называется рототабельным, если оценка дисперсии   y   в  любой точке зависит только от расстояния от центра плана.

          Если дисперсионная матрица плана (Х^ТХ)^-1 = а Е, где Е – единичная матрица, то такой план не только ортогонален, но и рототабелен.

          6) План Х называется ненасыщенным,  если n > p+1,  где  n – размер матрицы, определяемый числом экспериментов, р + 1 – определяет число переменных x_i. Если n = p+1, то план – насыщенный.

          7) План X называется А – оптимальным, если дисперсионная матрица имеет минимальный след.

          8) План X называется D – оптимальным, если определитель дисперсионной матрицы минимален (или определитель информационной матрицы максимален).