Лабораторна робота №13
Тема: Однофакторний дисперсійний аналіз.
Мета: Отримання практичних навичок по проведенню однофакторного дисперсійного аналізу.
Опис ходу виконання:
Користуючись вказівками, що описані в методичних вказівках виконуємо індивідуальне завдання (варіант №4) за допомогою пакету Statgraphics.
В результаті отримуємо наступний вміст вікон:

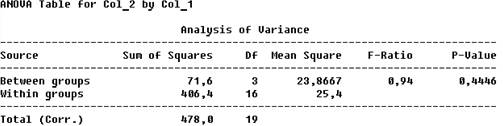
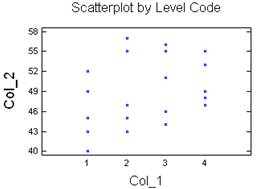
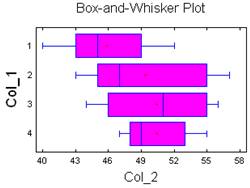
Наводимо вихідні дані у вигляді таблиці результатів експерименту:
|
|
Дані |
Сума |
Середнє |
|||||
|
1 |
49 |
40 |
43 |
52 |
45 |
229 |
45.8 |
|
|
2 |
43 |
55 |
45 |
57 |
47 |
247 |
49.4 |
|
|
3 |
56 |
46 |
44 |
51 |
55 |
252 |
50,4 |
|
|
4 |
47 |
49 |
53 |
48 |
55 |
252 |
50,4 |
|
|
980 |
49 |
|||||||
Математична модель однофакторного дисперсійного аналізу:
![]()
Складові частини математичної моделі:
![]() - помилка спостережень;
- помилка спостережень;
![]() - середнє значення вхідної величини;
- середнє значення вхідної величини;
а – величина, що характеризує ефективність і-го рівня фактору.
Запишемо
рівняння, що відповідають розсіюванню вихідних величин у відносно загального середнього
![]() і виразимо результат у вигляді суми
квадратів, зв’язаних між розсіюванням між рівнями факторів і суми квадратів, зв’язаних
з розсіюванням всередині окремих рівнів фактору:
і виразимо результат у вигляді суми
квадратів, зв’язаних між розсіюванням між рівнями факторів і суми квадратів, зв’язаних
з розсіюванням всередині окремих рівнів фактору: ![]() .
.
![]() -характеризує повну дисперсію
-характеризує повну дисперсію
![]() -характеризує дисперсію між
рівнями фактора А
-характеризує дисперсію між
рівнями фактора А
![]() -характеризує дисперсію
всередині рівня фактору.
-характеризує дисперсію
всередині рівня фактору.
![]()
![]()
![]()
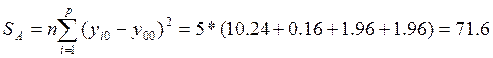
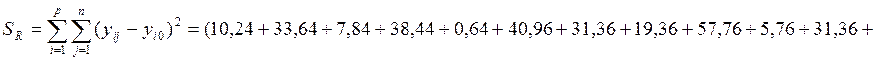
![]()
 При розрахунку
загальної дисперсії між рівнями фактору:
При розрахунку
загальної дисперсії між рівнями фактору: 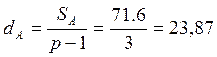
При
розрахунку загальної дисперсії всередині фактору: 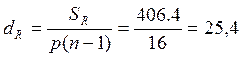
При
розрахунку повної дисперсії: 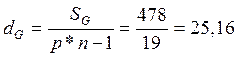
Якщо
дисперсія результатів вимірювань між рівнями фактору більша, ніж дисперсія
вимірювань всередині рівня, то вважають, що рівні оказують суттєвий вплив. Для
порівняння значень використовується критерій Фішера: 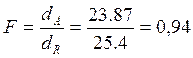 .
.
Запишемо розраховані дані в таблицю:
|
Компоненти дисперсії |
Сума квадратів |
Число степенів свободи |
Серднєквадр. відхилення |
Відношення Фішера |
Рівень значущості |
|
Між рівнями фактору |
71.6 |
3 |
23,87 |
0,94 |
|
|
Всередині фактору |
406,4 |
16 |
25,4 |
||
|
Повна дисперсія |
478 |
19 |
Гіпотези:
За
основну гіпотезу приймається гіпотеза про те, що різниця між дисперсією між
рівнями фактору і всередині фактору несуттєва, при ![]()
Альтернативна:
різниця між дисперсією між рівнями фактору і всередині фактору суттєва,
при ![]() .
.
![]()
![]()
![]()
Висновок: В результаті виконання лабораторної роботи отримані практичні навички по проведенню однофакторного дисперсійного аналізу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.