Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 9

Легко получить формулу, связывающую преобразование Фурье от последовательностей на разных этапах разбиения:

		(2.22)
	(2.23)

где  и  – спектральная плотность для четных и нечетных отсчетов сигнала.

Количество четных или нечетных отсчетов равно . Для спектральных плотностей  и  количество отсчетов, согласно формуле (2.15), также равно . Поэтому необходимо получить формулу для отсчетов спектральной плотности  при :

	(2.24)
	(2.25)

где .

Формулы (2.23) и (2.25) определяют основную операцию, которую необходимо выполнять несколько раз для получения БПФ. Эту операцию можно изобразить в виде графа:

 

Рис. 2.3 Базовая операция «Бабочка» для алгоритма с прореживанием по времени

Она получила название базовая операция «Бабочка» за подобие изображения ее графа четвероклылому насекомому. Здесь .

Из «Бабочек» можно составить граф для любого N. Например, если , граф будет выглядеть следующим образом:

 

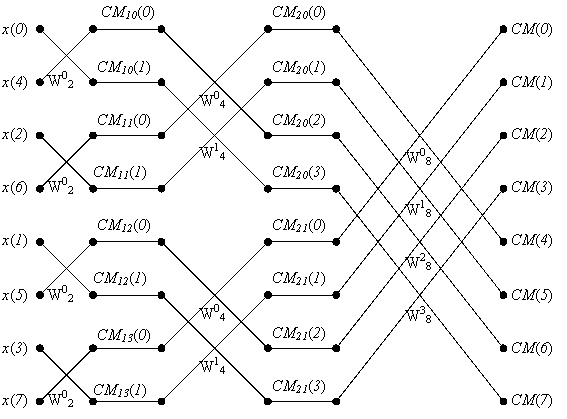Рис. 2.4 Граф алгоритма БПФ с прореживанием по времени при N = 8

2.3.2  Алгоритм с прореживанием по частоте

Идея алгоритма Кули-Тьюки по основанию 2 с прореживанием по частоте заключается в поэтапном разбиении выходной последовательности спектральной плотности на четные и нечетные отсчеты. Разбиение аналогично разбиению входных отсчетов.

Базовая операция «Бабочка» для данного алгоритма основывается на следующих формулах:

(2.26)

Для четных отсчетов спектральной плотности:

(2.27)