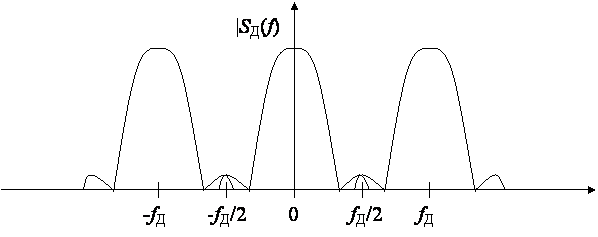Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 6

 

Рис. 2.2 Наложение копий спектра при недостаточно высокой частоте дискретизации

2.2  Дискретное преобразование Фурье

При разложении сигнала в ряд Фурье он должен быть периодическим. Предположим, что период сигнала s(t) равен ND . Тогда ряд Фурье будет иметь вид:

(2.1)

Подставим модель дискретного сигнала (2.2) в формулу (2.1) и после преобразований получаем формулу дискретного преобразования Фурье:

(2.2)

При ограничении сигнала во времени пределы суммирования естественно могут быть также ограничены областью определения сигнала. Это уже не периодический, а ограниченный во времени сигнал (импульсный). Формула (2.2) примет вид:

(2.3)

Ограничение сигнала приводит к ограничению комплексных экспонент (базисных функций ряда Фурье). Количество экспонент сокращается до N, (по причине периодичности спектральной плотности (2.5)). Поэтому в формуле ряда Фурье для ограниченного во времени дискретного сигнала количество коэффициентов равно N:

(2.4)

Согласно обобщенному ряду Фурье любой сигнал может быть разложен в любом выбранном ортогональном базисе:

(2.5)

Базисом называют совокупность ортогональных функций . Возможно дополнительное условие – нормированность базиса. Это означает, что энергия каждой функции базиса должна быть равна 1:

(2.6)

Для комплексного ряда Фурье гармонический базис имеет вид (согласно формуле (2.3)):

(2.7)

где N - число отсчетов цифрового сигнала и количество базисных функций;

n - дискретное время;

k - дискретная частота.

Благодаря коэффициенту  базис не является нормированным. Чтобы он был нормирован необходимо функцию умножить на :

(2.8)

Операция вычисления коэффициентов разложения C(k) в гармоническом базисе получила название ПРЯМОЕ ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ или, чаще говорят - ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (ДПФ). Коэффициенты C(k) определяется следую­щими выражениями: