Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 5

 Следует иметь в виду, что форма АЧХ ФНЧ в формулах (1.11) и (1.12) не учитывается и оценка влияния частоты дискретизации имеет погрешность. Для более точной оценки нужно учитывать степень подавления шума во всем диапазоне частот.

2  Цифровой спектральный анализ

2.1  Спектр дискретного сигнала

Математическая модель дискретного сигнала может быть получена на основе фильтрующего свойства дельта-функции. Согласно этому свойству аналоговый (непрерывный) сигнал имеет динамическое представление:

(2.1)

Поскольку дискретный сигнал определен только в точках t_n = nD интегрирование в формуле (2.1) можно заменить суммированием по индексу n. Дифференциал при этом заменяется на D:

(2.2)

Сумма, входящая в выражение (2.2) есть модель идеальной дискретизирующей последовательности. Эта сумма является периодическим сигналом и, следовательно, может быть представлена рядом Фурье. Коэффициенты ряда равны:

(2.3)

В формуле (1.3) было учтено, что в интервал интегрирования (-D/2, D/2) попадает только одна дельта-функция при n = 0. Тогда математическая модель дискретного сигнала (1) записывается в виде:

(2.4)

Умножение сигнала на соответствует сдвигу спектральной плотности на , поэтому спектр дискретного сигнала записывается через спектр аналогового сигнала  следующим образом:

(2.5)

 Итак, спектр дискретного сигнала периодический. Период равен  по круговой частоте и  при циклической частоте, где f_Д - частота дискретизации. Число периодов бесконечно (рис. 2.1) и это означает, что если  дискретизировать сигнал, сдвинутый по частоте на f_Д , то спектр сигнала будет тот же. Таким образом, подтверждается еще раз правильность теоремы Котельникова, ограничивающей диапазон частот преобразуемого сигнала. Кроме того, если нарушить теорему, то копии периодов будут как бы налагаться друг на друга (рис. 2.2) (наложение – aliasing), что свидетельствует о появлении ложных частотных составляющих. Для предотвращения нарушения теоремы, перед дискретизацией сигнал анализируется, а при необходимости фильтруется так, чтобы сигнал практически не содержал частот выше  (фильтр называется антиэлайзинговым (antialiasing)).

 

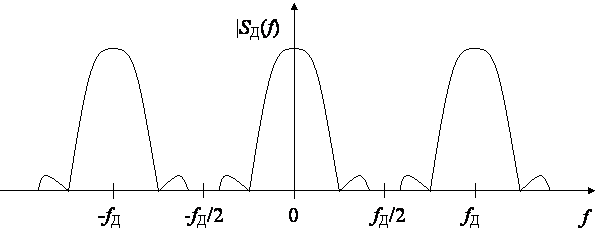Рис. 2.1 Спектр дискретного сигнала