Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 11

Как можно догадаться, системная функция есть передаточная функция фильтра форме  Z-преобразования. Для перехода к форме преобразования Фурье используются формулы перехода:

(3.3)

где 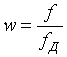 – частота нормированная на частоту дискретизации.

Последняя формула предпочтительна для общего случая, поскольку нормированная частота w делает фильтр подходящим для любой частоты дискретизации.

4  КИХ-фильтры с линейной ФЧХ

Для того, чтобы КИХ-фильтр имел линейную ФЧХ, импульсная характеристика фильтра должна быть симметричной

(4.1)

или  антисимметричной

(4.2)

относительно середины. В этом случае все зависит от порядка фильтра М (четное или нечетное число). Если порядок М – четное, то количество отсчетов нечетное, следовательно, появится средний отсчет, относительно которого и будет зеркальная симметрия. При нечетном М линия пройдет между отсчетами     и  .

Коэффициент передачи фильтра может быть получен как переход от системной функции к частотному коэффициенту передачи. При этом следует использовать нормированную частоту:

(4.3)

(4.4)

Формула (4.4) справедлива для М четного. Дальнейшее преобразование сводится к умножению и делению на функцию .

(4.5)

(4.6)

(4.7)

Используем экспоненциальную запись комплексного числа

(4.8)

Можно сделать вывод о модуле и фазе комплексного коэффициента передачи. ФЧХ:

(4.9)

Групповое время задержки – производная ФЧХ по частоте:

рад ( отсчетов)

(4.10)