Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 15

Структурная схема БИХ-фильтра можно построить исходя из разностного уравнения (Рисунок 7.1):

 

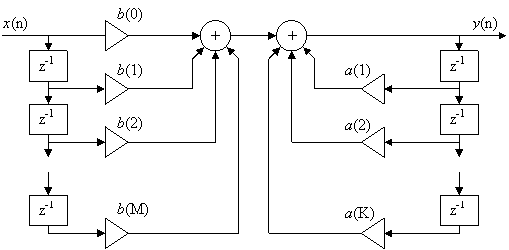Рис. 7.1 Прямая форма БИХ-фильтра

 

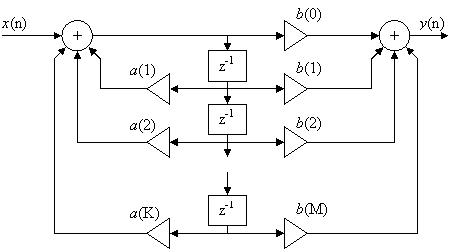Рис. 7.2 Каноническая форма БИХ-фильтра

Отделив рекурсивную часть фильтра от трансверсальной и, используя формулу последовательного соединения фильтров, можно получить  другую структурную схему, которая называется канонической (Рисунок 7.2).

Каноническая форма использует одни и те же элементы задержки для рекурсивной и трансверсальной части. Это определяет ее эффективность в смысле меньшего объема памяти, но по количеству операций схема может оказаться не эффективной. Элементная база ЦОС также сильно влияет на эффективность. Поэтому лучше иметь представление о разных структурах фильтров и выбирать их в соответствии с элементной базой (или может быть исходя из иных соображений). Вообще есть возможность устанавливать фрагменты фильтров последовательно и параллельно. Важно при этом, чтобы результирующее разностное уравнение определяло требуемые параметры фильтра (АЧХ, ФЧХ, импульсную характеристику).

Как известно, при последовательном соединении (Рисунок 7.3) системные функции фильтров перемножаются, при параллельном (Рисунок 7.4) – складываются, а при обратной связи (Рисунок 7.5) соответствуют выражению:

,

(7.6)

 

Используя правила различных соединений фильтров можно получить еще одну форму структурной схемы БИХ-фильтра – транспонированную (Рисунок 7.6).

Если системную функцию преобразовать так, чтобы числитель и знаменатель вместо полиномов степени М и К будет стоять произведение полиномов первого и второго порядков, то структурную схему фильтра можно заменить последовательным соединением фильтров 1-го и 2-го порядков. Необходимо реализовать фильтр высокого порядка, а количество разрядов, используемое для коэффициентов фильтра и отсчетов недостаточно для точного их представления. Чем больше номер коэффициента в рекурсивной части, тем сильнее его влияние на импульсную характеристику, поэтому квантование может привести к потере устойчивости. Квантование отсчетов так же приводит к потере устойчивости, но эффект такого квантования другой, он называется предельным циклом.

 

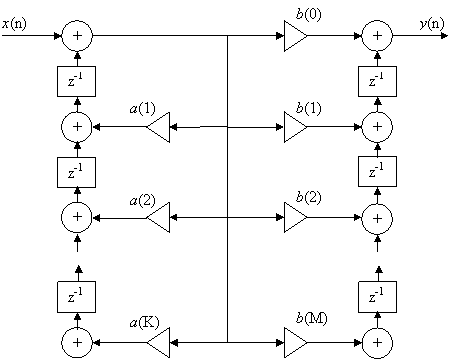Рис. 7.6 Транспонированная форма БИХ-фильтра

8  Синтез БИХ-фильтров

8.1  Метод инвариантных частотных характеристик (билинейное преобразование)

Метод основан на характеритсиках уже рассчитанных аналоговых фильтров. Комплексный коэффициент передачи преобразуется к системной функции цифрового фильтра через биполярное преобразование:

,

(8.1)

z – оператор Z-преобразования;