Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 14

Следующий пример – фильтр преобразователь Гильберта (Hilbert Transformer). Этот фильтр можно получить, отталкиваясь от частотной характеристики аналогового прототипа:

,

(6.3)

За счет преобразования Фурье получаем следующую аналоговую импульсную характеристику:

,

(6.4)

Дискретизируя эту функцию с шагом 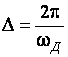   получаем дискретную импульсную характеристику:

,

(6.5)

Такой фильтр имеет нулевые коэффициенты через один отсчет.

7  БИХ-фильтры

БИХ-фильтр с бесконечной импульсной характеристикой. Разностное уравнение фильтра:

(7.1)

b и a – коэффициенты фильтра,

x – входные отсчеты

y – выходные отсчеты.

М и К – порядок трансверсальной и рекурсивной части. Наибольшее значение из К и М будет являться порядком фильтра в целом. Иногда возможно добавление в формулу еще одного слагаемого а(0)y(n), где а(0) – коэффициента усиления. Это слагаемое будет означать, что сумма в выражении (7.1) будет начинаться с 0, а не с 1.

Если отсутствует трансверсальная часть, то все коэффициенты b(m) = 0, а БИХ – фильтры называются чисто рекурсивными (или только полюсными).

Применяя Z-преобразование к разностному уравнению получим системную функцию для БИХ-фильтров:

,

(7.2)

БИХ-фильтр имеет М нулей и К  полюсов. Полюсы фильтра определяют его устойчивость. Для того, чтобы фильтр был устойчивым необходимо, чтобы его импульсная характеристика была затухающей функцией, тогда после снятия любого входного воздействия, выходной сигнал будет затухать до нуля.

Системная функция может быть записана как:

,

(7.3)

 - значение полюса передаточной характеристики.

Импульсная характеристика будет иметь вид:

(7.4)

Убывающей  будет в этом случае, если полюсы по модулю будут меньше единицы:

(7.5)

Иначе можно сказать, что все полюсы должны находиться на комплексной плоскости на круге с единичным радиусом.