Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 13

Рис. 3.1 Требуемая АЧХ фильтра типа ФНЧ

Весовая функция q является относительной величиной, абсолютное её значение не имеет никакого смысла. Если установим в полосе пропускания  (ПП) q=10, а в полосе задержки q=1, то в ПП точность аппроксимации будет в 10 раз выше. В ПП  q можно сделать равной нулю, т.е. q в ПП не будет учитываться при синтезе фильтра.

5.3  Метод равномерной аппроксимации (Equripple)

Целевая функция:

,

(5.3)

 означает, что модуль отклонения аппроксимируемой кривой от требуемой должен быть минимальным на всех частотах. Чебышевым была доказана теорема, что минимум достигается, если аппроксимирующая функция будет периодически отклоняться от аппроксимируемой (М+2) раза, причем модули этих отклонений должны быть одинаковыми.

Задача нахождения аппроксимируемой кривой может быть решена любым методом оптимизации (метод сопряженных градиентов и др.). Но наиболее эффективным методом, с учетом использования теоремы Чебышева, является метод Ремеза.

Точки максимального отклонения аппроксимирующей кривой были названы Чебышевым точками альтернанса. В частотных областях, где функция  q больше, точки альтернанса смещается больше.

5.4  Сравнительная характеристика методов синтеза КИХ – фильтра

Предпочтение какого – либо метода перед другими двумя не найдено: причина в многообразии целей проектирования, например, в полосе задержки важно, чтобы затухание было равномерным на всех частотах, а для других – затухание увеличивается с уменьшением частоты. Поэтому рекомендуется, если нет ограничений на время разработки, рассчитать по всем трем методам, а затем выбрать лучший.

6  Примеры широкоиспользуемых КИХ – фильтров:

Наиболее часто используются КИХ – фильтры с прямоугольной импульсной характеристикой. Такой фильтр называется однородным.

 

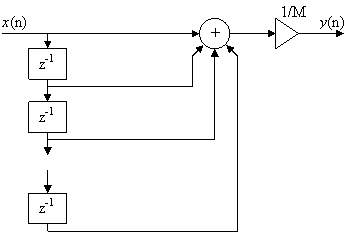Рис. 6.1 Однородный фильтр

Разностное уравнение для него должно быть следующим:

,

(6.1)

 где  – масштабирующий множитель.

На рисунке 6.2 приведена более эффективная схема однородного фильтра, указывающая на способ экономной реализации за счет операций только с первым и последним отсчетами в памяти фильтра. Согласно этой схеме системная функция фильтра равна:

,

(6.2)

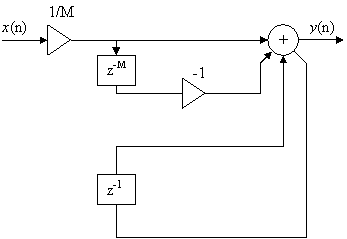
Рис. 6.2 Эффективная схема однородного фильтра

Этот КИХ – фильтр может использоваться для понижения шума в системах, в которых не хватает вычислительной мощности.

Представляет интерес, также, последовательное соединение двух однородных фильтров. Образованный, таким образом, фильтр называется триангулярным.

Импульсная характеристика фильтра получается треугольной, откуда и следует название фильтра. Этот фильтр имеет более высокое затухание в полосе задерживания.