Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 16

p – оператор преобразования Лапласа;

 – любое положительное число.

Рассмотрим этот процесс для одного из видов аналоговых фильтров – фильтров Баттерворта.

По виду фильтры делят  на низкочастотные (НЧ), высокочастотные (ВЧ), полосовые фильтры (ПФ), режекторные фильтры (РФ). Между этими фильтрами есть связь как в области преобразования Лапласа, так и в области z-преобразования, поэтому рассмотрим только один из видов – фильтры нижних частот (ФНЧ). Другие фильтры могут быть получены на основе перехода от одного фильтра к другому.

Для фильтра Баттерворта коэффициент передачи в форме преобразования Лапласа:

,

(8.2)

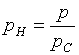 - нормированный на частоту среза оператор Лапласа;

k – порядок фильтра.

Благодаря плоской АЧХ этот фильтр называется еще фильтром с максимально-плоской характеристикой. Если приравнять знаменатель к нулю, то можно получить полюсы функции в форме преобразования Лапласа:

,

(8.3)

,

,

(8.4)

Формула (8.4) определяет полюсы коэффициента передачи аналогового фильтра по мощности. Для устойчивости фильтра выбирают полюсы, которые лежат в левой полуплоскости (Рисунок 8.1).

Если порядок фильтра нечетный, то имеется один действительный полюс, остальные – комплексно-сопряженные. При четном порядке действительных полюсов нет. Кроме того, согласно формуле (8.4), полюсы находятся на одинаковом угловом расстоянии и их модули равны нулю. Иными словами, все полюсы лежат на окружности единичного радиуса с центром в начале координат.

 

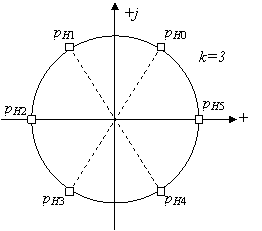Рис. 8.1 Расположение полюсов фильтра Баттерворта

Применив к формуле (8.2) билинейное преобразование (8.1), необходимо преобразовать полученное выражение к стандартному виду системной функции (7.2). Это сделать не всегда просто. Поэтому возможен еще один вариант альтернативных действий. Используя обратное билинейное преобразование, можно получить полюсы системной функции:

,

(8.5)

Если известны полюсы системная функция может быть найдена по формуле:

,

(8.6)

Полученное выражение необходимо также преобразовать к стандартному виду системной функции (7.2).

Кроме того, во всех случаях, необходимо использовать только полюсы лежащие в левой полуплоскости преобразования Лапласа с номерами n₁…n₂.