Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 10

Для нечетных отсчетов спектральной плотности:

(2.28)

Далее все очевидно.

Операция «Бабочка» будет иметь вид:

 

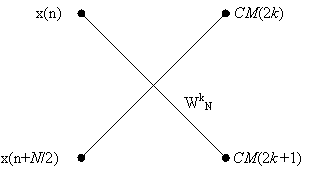Рис. 2.5 Базовая операция «Бабочка» для алгоритма с прореживанием по частоте

Для , граф БПФ представлен на рис. 2.6.

Прореживание по частоте позволяет построить эффективный алгоритм оценки частоты гармонического сигнала, поскольку часть алгоритма может быть проигнорирована, если анализировать энергию отсчетов на каждом этапе преобразования.

2.4  Обратное преобразование Фурье

В заключение, отметим, что алгоритм БПФ применяется и для ОДПФ. Для этого нужно, в общем случае, сделать два преобразования комплексной последовательности в комплексно-сопряженную:

(2.29)

т.е. необходимо изменить знак мнимой части С(k), выполнить БПФ, а после преобра­зования Фурье восстановленный сигнал будет равен действительной части результирующей последовательности, если С(k) – зеркально симметрична относительно частоты N/2 или 0. Именно этот способ использован в блоке IFFT в simulink MatLab.

 

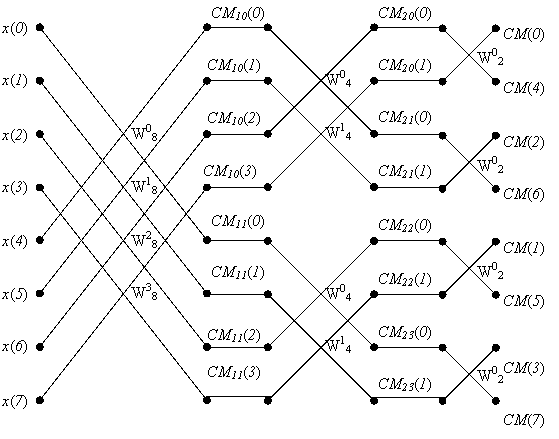Рис. 2.6 Граф алгоритма БПФ с прореживанием по частоте при N = 8

3  Фильтры с конечной импульсной характеристикой (КИХ- фильтры)

КИХ- фильтр строится на основе разностного уравнения:

(3.1)

где М – порядок КИХ фильтра.

Согласно формуле выходной сигнал фильтра есть дискретная свертка входного сигнала и импульсной характеристики  КИХ – фильтра. На основе (3.1) может быть построена структурная схема фильтра, она строится прямо по уравнению и поэтому называется прямой формой.

 

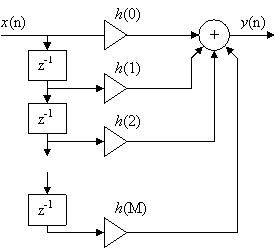Рис. 3.1 Структурная схема КИХ-фильтра (Прямая форма)

Отношение спектральных плотностей в форме Z-преобразования на входе и выходе фильтра называется системной:

(3.2)

Нулями системной функции (фильтра) называются значения z, при которых H(z)=0. Полюсами фильтра называются значения  z, при которых H(z)=∞. Следовательно, КИХ – фильтр имеет М – нулей и один М – кратный полюс в точке z=0.