Изучение материалла по курсу "Основы радиоэлектроники и связи", страница 12

Знак «минус» означает, что каждая составляющая спектра входного сигнала будет задержана на М/2 отсчетов. Если М – нечетное, то задержка будет равна нецелому числу отсчетов. При цифровой обработке сигналов чаще используется М – четное. Таким образом, КИХ – фильтры имеют точно линейную ФЧХ и не вносят фазовых искажений в фильтруемый сигнал, если его импульсная характеристика удовлетворяет условию симметричности или антисимметричности. Равенство коэффициентов для КИХ – фильтра означает упрощение разностного уравнения.

5  Синтез фильтров типа КИХ

5.1  Дискретизация импульсной характеристики (FIR Window)

Суть метода заключается в получении импульсной характеристики аналогового фильтра как преобразования Фурье от его АЧХ. ФЧХ будем считать линейной, а ещё лучше нулевой. Для того, чтобы ФЧХ оказалась нулевой, необходимо пронумеровать отсчеты: до середины импульсной характеристики отрицательные номера, после середины положительные. Приведем пример синтеза, в котором требуемая АЧХ имеет прямоугольную форму.

Метод дискретизации заключается в получении отсчетов аналоговой импульсной характеристики с интервалом дискретизации Δ. Чем больше отсчетов возьмем, тем ближе будет характеристика к прямоугольной форме. По факту импульсная характеристика перемножается на временное окно прямоугольной формы. В результате происходит эффект растекания АЧХ, также как имеет место эффект растекания спектра в спектральном анализе. Следовательно, и в данном примере, чтобы улучшить избирательные свойства фильтра прямоугольное окно следует заменить на специальное, например, на окно Хемминга.

5.2  Метод наименьших квадратов (Least - squares)

Для реализации метода устанавливается целевая функция следующего вида:

(5.1)

где w – нормированная частота;

– АЧХ синтезируемого фильтра;

– требуемая АЧХ фильтра;

 – весовая функция.

Цель найти коэффциенты фильтра, при которых G минимальна. Классический анализ основан на решении системы уравнений:

(5.2)

Из системы линейных уравнений (5.2) находятся коэффициенты .

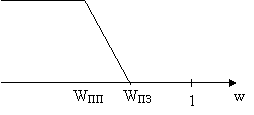
 может быть задана в виде кусочно – линейной функции.

   

	1

ПЗ

ПерП

ПП