Автоматическое управление техническими системами. Система «Управляемый преобразователь – машина постоянного тока» как объект управления. Автоматическое регулирование координат электропривода. Частотно токовое управление АД, страница 8

При переходе к участку II характеристики 3, стабилизирующие скорость обратные связи отключаются, и вводится в действие отрицательная обратная связь по моменту, т.е. изменяется структура системы, которая теперь будет работать в режиме автоматического регулирования момента двигателя, т.е. здесь регулируемая величина . При этом скорость двигателя представляет собой основное возмущающее воздействие (в установившемся режиме). При неподвижном двигателе Y_o¢¢ = М_о¢¢ = М¢¢_кз и управляющий сигнал. С увеличением скорости, благодаря действию регулирующей обратной связи по моменту, растет сигнал х¢¢, принимая последовательно значения, что соответствует переходу изображающей точки характеристики 3 по соответствующим характеристикам семейства Р. Поэтому на участке II значительные изменения скорости сопровождаются относительно небольшими изменениями момента. Перепад момента определяет здесь точность поддержания постоянства момента при изменении возмущающего воздействия от  до . Участок II предусматривается, например, для защиты механизма рулевого управления автомобиля при резком увеличении нагрузки на ЭМУР.

На обоих участках характеристики 3 система, изменяя структуру, остается статической. Для таких систем пользуются понятием статизма системы, который характеризуется величиной

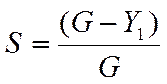                                                                                                  (3.1.)

Где G – заданное установившееся значение регулируемой величины; Y₁ - установившееся значение регулируемой величины, соответствующее неизменному во времени возмущающему воздействию F₁₍₁₎ (Рис. 3.1б).

Статизм может быть выражен как сумма статизма по заданию Sg и статизма по возмущению S_f :

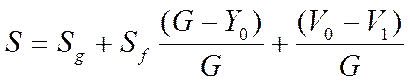                                                           (3.2.)

где – значение регулируемой величины при f₁ = о.

Статизм системы зависит от ее параметров, в первую очередь от коэффициента передачи разомкнутой системы:

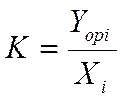                                                                                                     (3.3.)

Где Xiи Yopi – соответственно значения управляющего сигнала и регулирований величины при f₁ = о для i – й характеристики разомкнутой системы.

Для оценки наклона участка статической характеристики удобнее пользоваться понятием статизма характеристики.

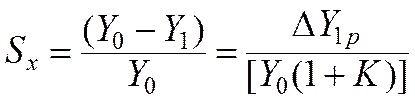                                                                   (3.4.)

В системах, астатических по возмущению f₁, значения S_f и S_х  равны нулю.

Таким образом, путем выбора соответствующих обратных связей и значений коэффициента передачи системы в замкнутых системах П-Д можно формировать статические характеристики практически любого вида.

Динамические характеристики замкнутых систем П-Д характеризуют поведение этих систем в переходных процессах пуска, торможения, регулирования скорости, сброса и наброса нагрузки и т.п., то есть, при изменениях управляющего или возмущающего воздействия. Это характеристики w = f(t); М = f(t); и т.д.

Работы с АСУЭП можно разделить на два направления: анализ, то есть исследование готовой системы с целью определения ее свойств и пути их улучшения, и синтез, то есть проектирование системы, удовлетворяющей поставленным требованиям. В обоих случаях принято рассматривать динамику систем в условиях детерминированных внешних воздействий. Наиболее часто используют воздействия в виде ступенчатой функции  и .

где 1(t) – единичная ступенчатая функция.

На Рис. 3.2. показана кривая изменения регулируемой величины y или ее приращения Dy в переходном процессе, обусловленном мгновенным приращением DG задающего воздействия в момент времени t = 0, то есть кривая, характеризующая реакцию системы на скачок DG×1(t).

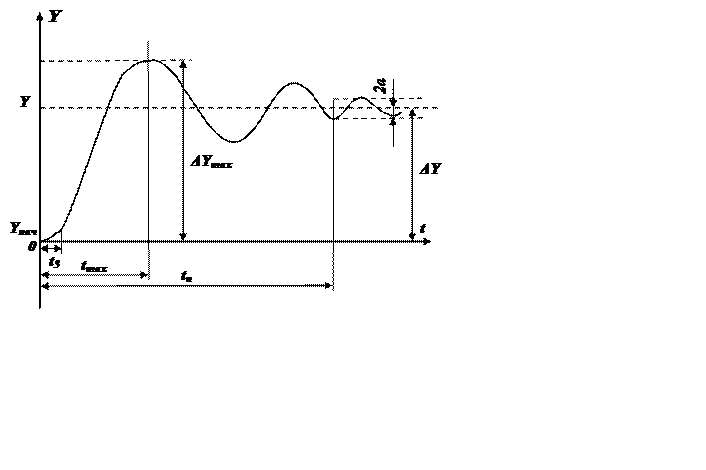
Рис. 3.2

Предполагается, что при t < 0 система работала в установившемся режиме. При DG = 1 кривую y(t) называют переходной характеристикой или переходной функцией h_g(t). При скачке возмущающего воздействия DF1×1(t) для случая        DF₁ = 1 получается переходная функция hf(t).