1. магнитная проницаемость стали равна бесконечности;
2. распределение полей самоиндукции статора и возбуждения вдоль окружности статора – синусоидальное;
3. фазовые обмотки – симметричны.
Опустив промежуточные выкладки, приведем систему уравнений СДМВ в осях d и q.
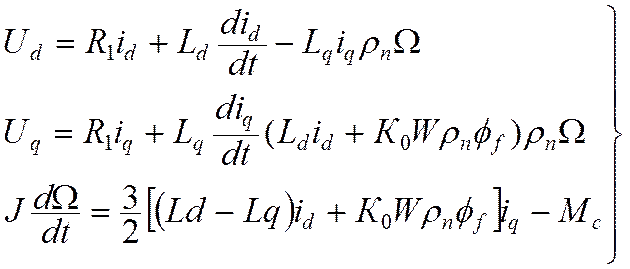 (12.1)
(12.1)
Здесь R1 – активное сопротивление фазной обмотки статора;
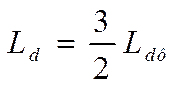 - собственная индуктивность продольного контура;
- собственная индуктивность продольного контура;
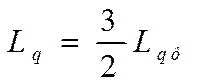 - собственная индуктивность поперечного контура;
- собственная индуктивность поперечного контура;
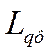 ,
, 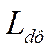 - индуктивность фазы при совпадении оси
обмотки фазы статора с продольной осью индуктора и с поперечной осью индуктора;
- индуктивность фазы при совпадении оси
обмотки фазы статора с продольной осью индуктора и с поперечной осью индуктора;
![]() - число пар полюсов;
- число пар полюсов;
![]() - число витков фазной обмотки;
- число витков фазной обмотки;
![]() - коэффициент приведения;
- коэффициент приведения;![]()
![]() - поток индуктора на полюс;
- поток индуктора на полюс;
Структурная схема СДМВ в
осях ![]() приведена на рис.12.1
приведена на рис.12.1
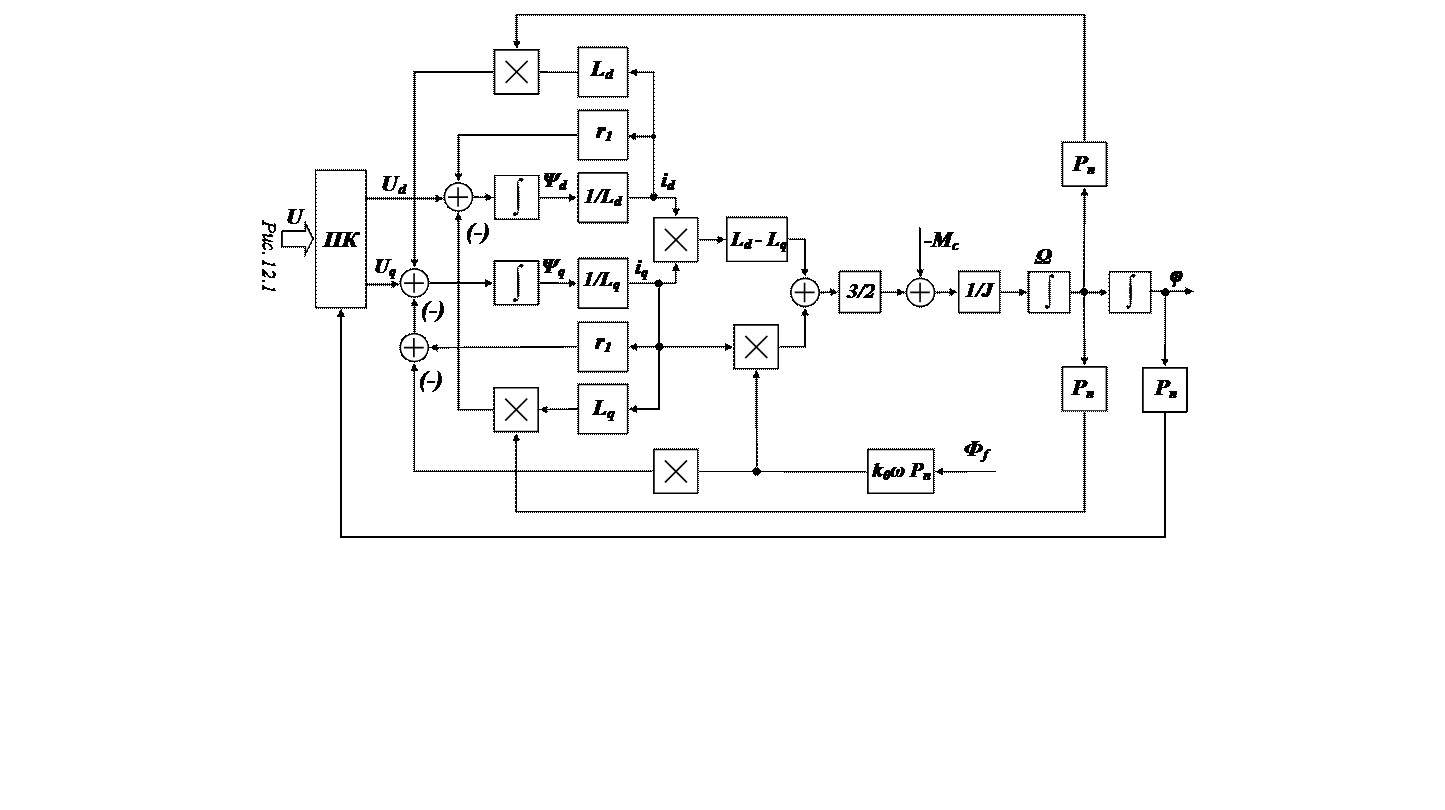
Здесь ПК – преобразователь координат.
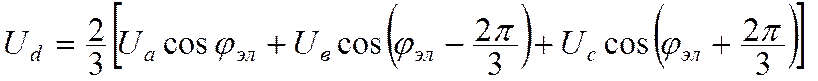 (12.2)
(12.2)
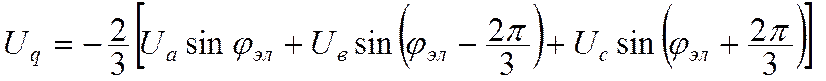 (12.3)
(12.3)
При настроении реальных систем ЧТУ регулирование токов ведут в неподвижной системе координат, и тогда более удобной является структурная схема, где часть переменных представлена в неподвижной системе координат (рис.12.2)

Рис. 12.2
Обозначим:
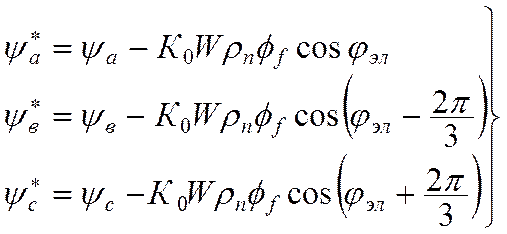 (12.4)
(12.4)
Следовательно,
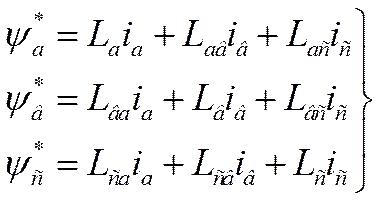 (12.5)
(12.5)
т.е.
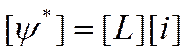 (12.6)
(12.6)
где 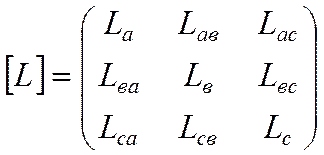
тогда 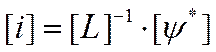 (12.7)
(12.7)
Полная система уравнений:
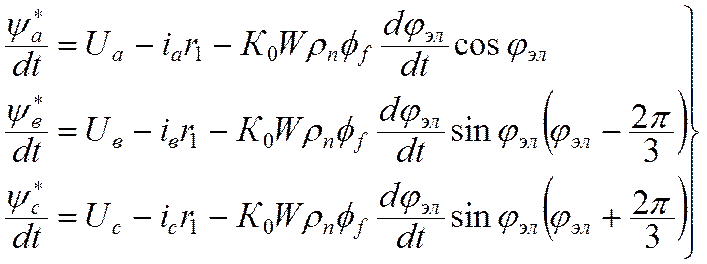
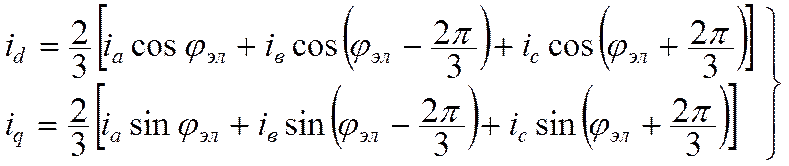
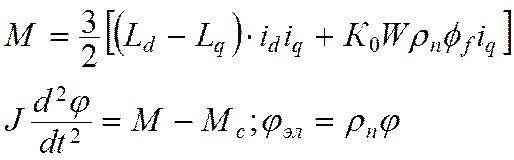
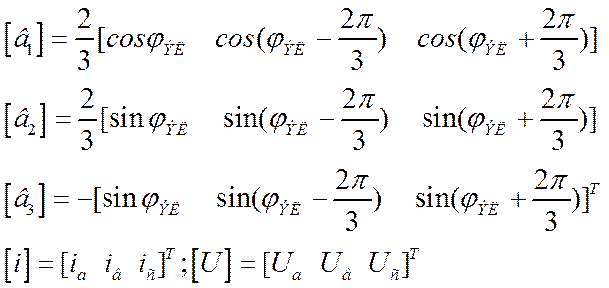
Как уже отмечалось, для управления моментом, а, следовательно, и скоростью бесколлекторного двигателя необходима система управления, преобразующая сигнал задания требуемого момента и информацию о состоянии двигателя в сигналы задания управляющих воздействий, воспринимаемых двигателем. Причем, на показатели качества электропривода существенное значение оказывают принципы построения этой системы.
Управлять СДМВ можно, формируя сигналы задания тока
в разных системах координат: 2-х фазной в осях d и q, полярной с помощью модуля и угла вектора тока трехфазной
а, в, с, и неподвижной в осях ![]() ,
,![]() .
.
Рассмотренные системы координат могут использовать различные варианты регуляторов: двухпозиционные (релейные) и квазенепрерывные равных (П; ПИ; ПИД и т.п)
Кроме того, для рассмотренных сигналов управления возможны два вида модуляции: векторная и пофазная. Классификация алгоритмов управления представлена в таблице 12.1. Функциональные схемы показаны на рисунках 12.3 – 12.14. (Материал по классификации разработан Б.М. Боченковым, доц. каф ЭОПУ)
Таблица.12.1
|
Вариант регулятора тока |
Тип модуляции |
Система координат, в которой ведётся регулирование токов |
|||
|
Вращающаяся ортогональная d;q |
Неподвижная ортогональная α;β |
Неподвижная трехосевая a;b;c |
Полярная Im;ε |
||
|
2х позиционый |
рис.12.3. |
рис.12.4. |
рис.12.5. |
рис.12.6. |
|
|
квазинепрерывный |
Векторная |
рис.12.7. |
рис.12.8. |
рис.12.9. |
рис.12.10. |
|
Пофазная |
рис.12.11. |
рис.12.12. |
рис.12.13. |
рис.12.14. |
|
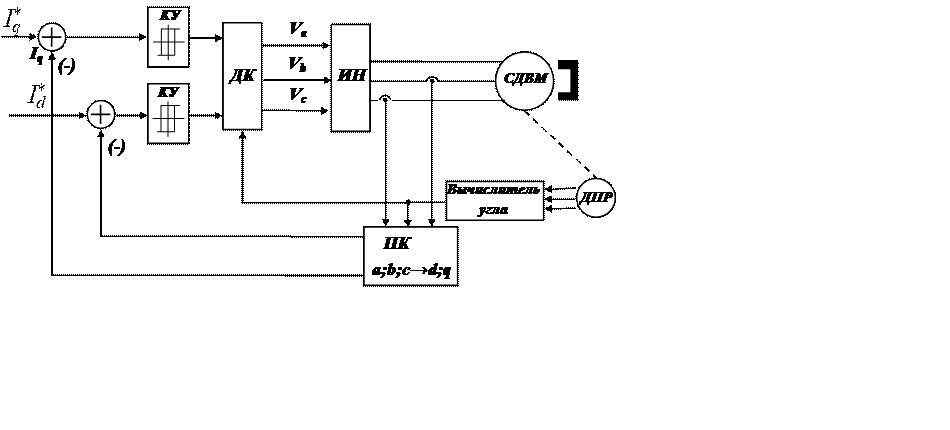
Рис. 12.3 Система управления со скользящими режимами в системе координат d и q.
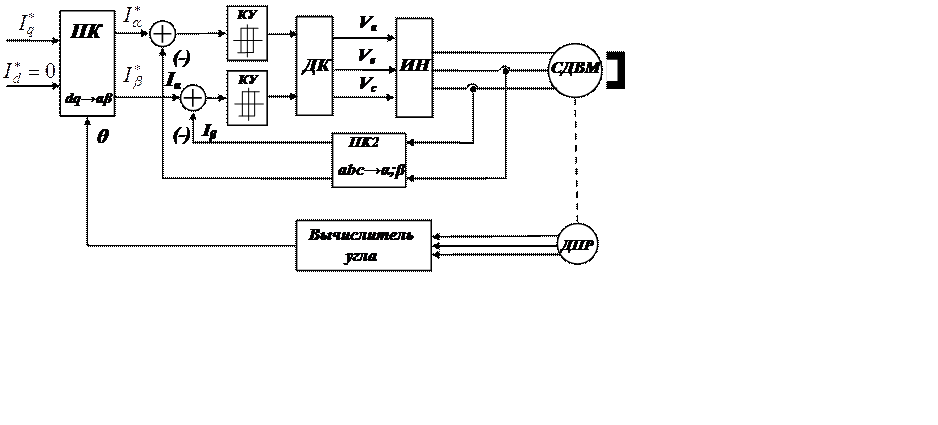
Рис. 12.4 Система управления со скользящими режимами в системе координат α и β.
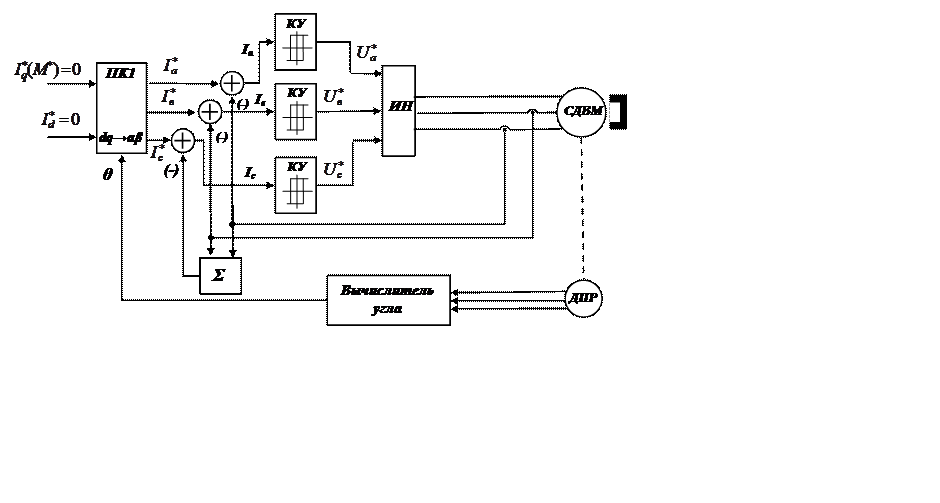
Рис. 12.5 Система управления со скользящими режимами с регулированием тока в осях а, в, с.
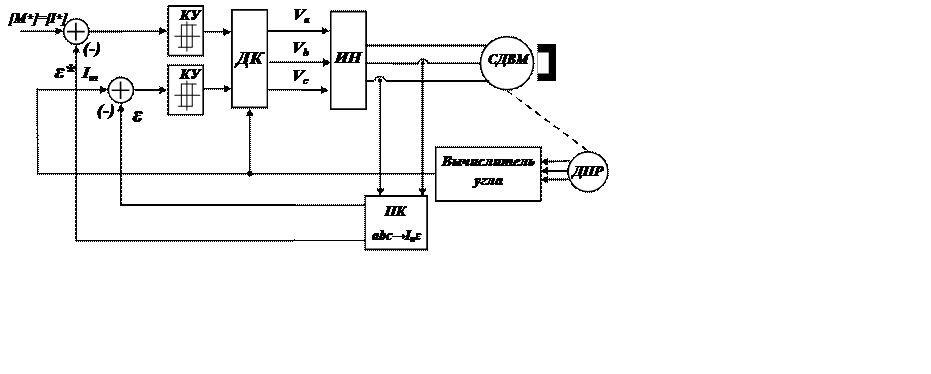
Рис. 12.6 Система управления со скользящими режимами в полярной системе координат.
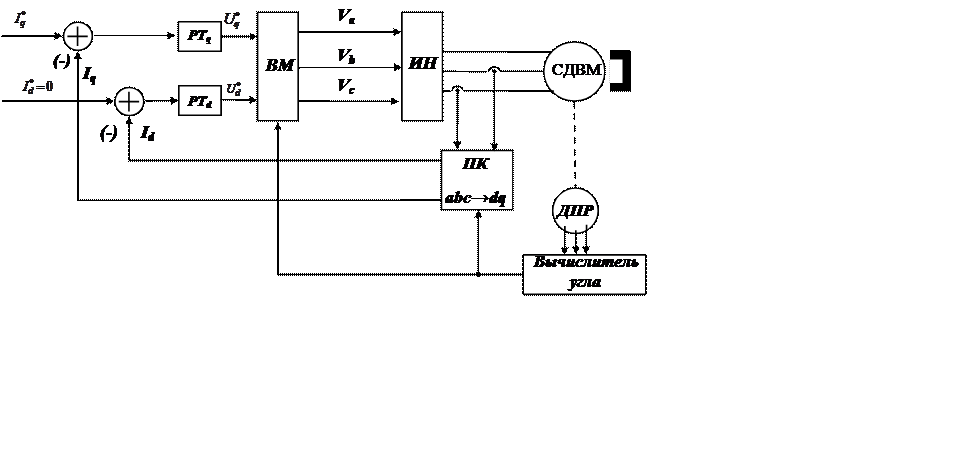
Рис. 12.7 Система управления с векторной модуляцией в осях d и q.
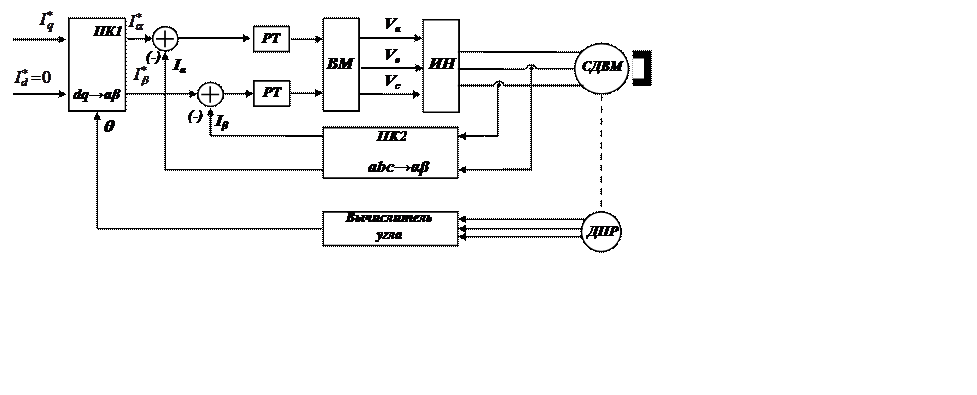
Рис. 12.8 Система управления с векторной модуляцией в неподвижной системе координат α и β.
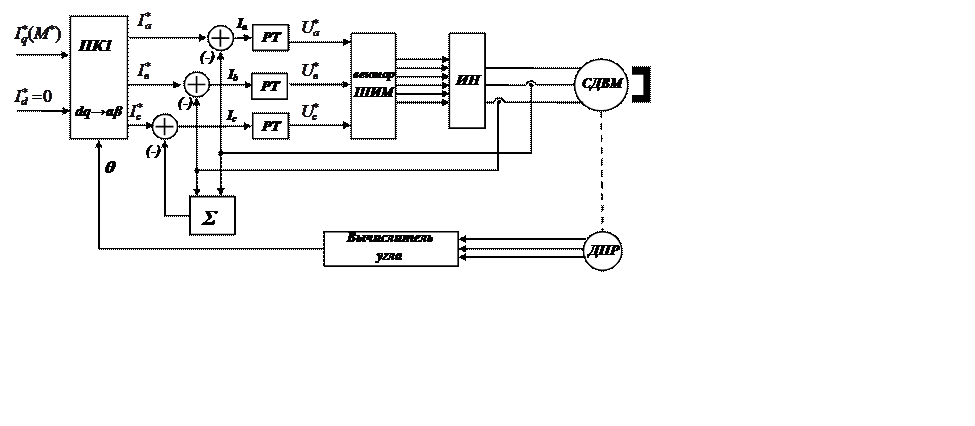
Рис. 12.9 Система управления с регулированием тока осях а, в, с и векторной модуляцией.
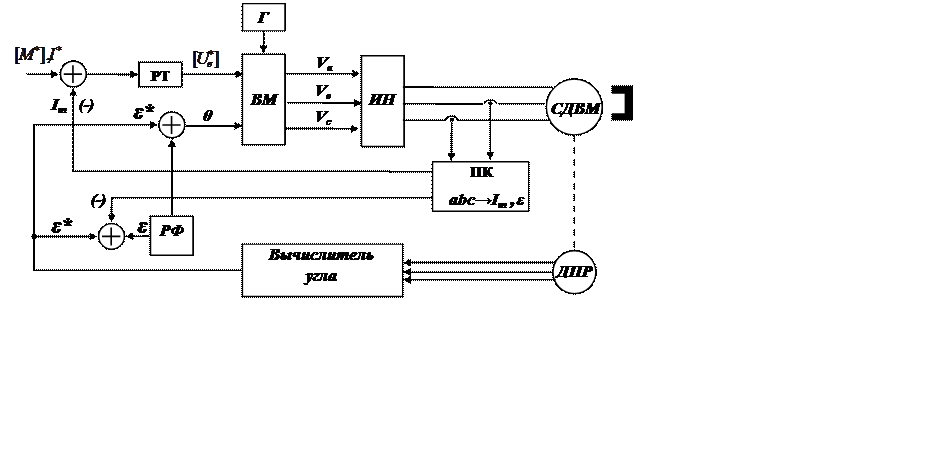
Рис. 12.10 Система управления с векторной модуляцией в полярной системе координат.
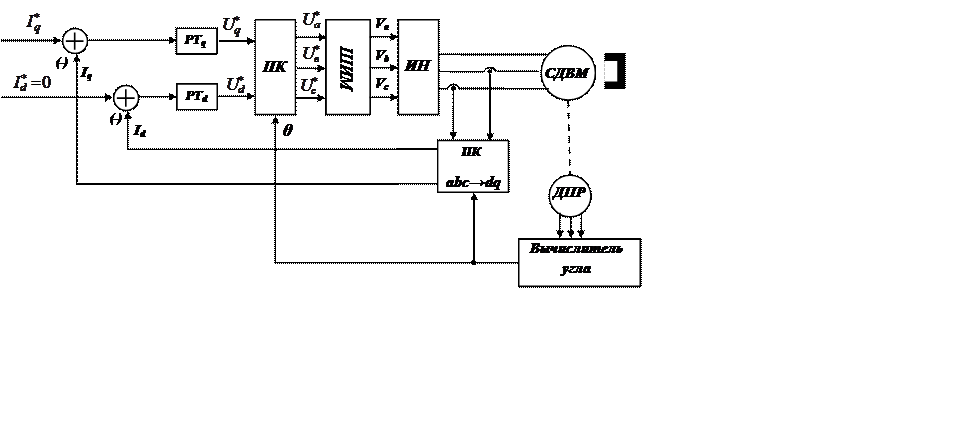
Рис. 12.11 Система управления с пофазной модуляцией в системе координат d и q.
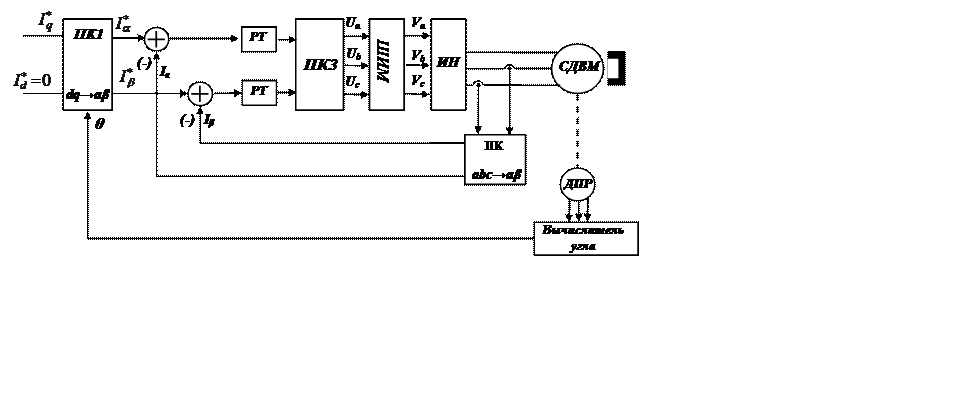
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.