Представив реальные
переменные в виде векторов будем полагать, что преобразованные переменные в
осях ![]() пропорциональны сумме проекций реальных
переменных
пропорциональны сумме проекций реальных
переменных ![]() на оси
на оси ![]() и
и![]() .
. 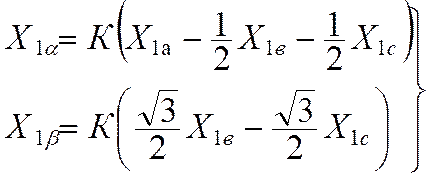
![]() (10.1)
(10.1)
где ![]() -
согласующий коэффициент, обеспечивающий инвариантность мощности. Выполненные
преобразования иллюстрируются на рис.10.1.
-
согласующий коэффициент, обеспечивающий инвариантность мощности. Выполненные
преобразования иллюстрируются на рис.10.1.

Рис. 10.1
При симметричной трехфазной системе векторов:
![]() (10.2)
(10.2)
и
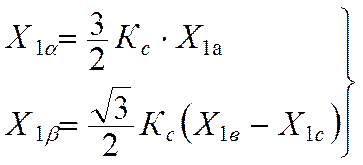 (10.3)
(10.3)
Аналогично
определяются ![]() и
и
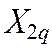 для роторной
цепи машины.
для роторной
цепи машины.
Обратное преобразование осуществляется по выражениям:
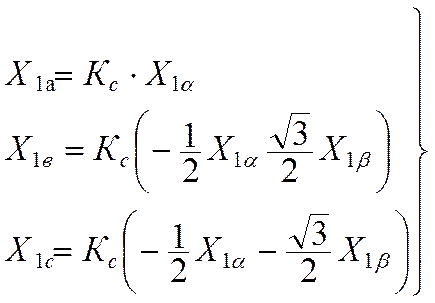 (10.4)
(10.4)
Для определения значения ![]() ,
обеспечивающего выполнение условия инвариантности мощности при преобразовании
координат, определим мощность, потребляющую обмотками статора.
,
обеспечивающего выполнение условия инвариантности мощности при преобразовании
координат, определим мощность, потребляющую обмотками статора.
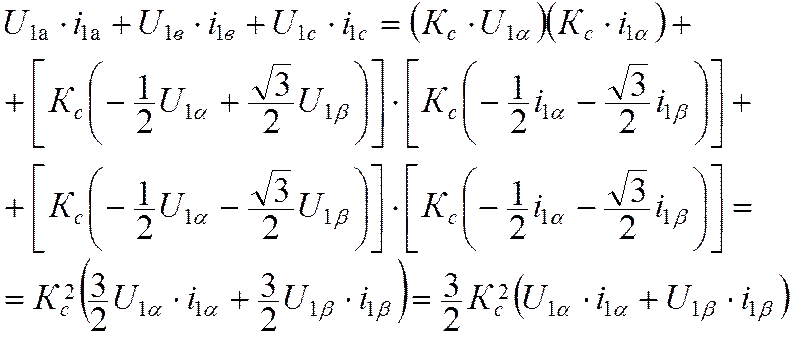 (10.5)
(10.5)
Следовательно, для выполнения условий инвариантности мощности необходимо, чтобы:
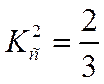 или
или 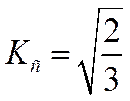 (10.6)
(10.6)
Тогда
![]() (10.7)
(10.7)
т.е. обеспечивается инвариантность мощности в различных системах координат.
Недостатком матописания обобщенной электрической
машины в виде (1.7) является наличие произведения переменных, периодических
коэффициентов, меняющихся в связи с зависимостью собственных и взаимных
индуктивностей машины от 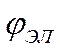 , что значительно усложняет
задачи анализа и синтеза САУ.
, что значительно усложняет
задачи анализа и синтеза САУ.
Решение этих задач можно упростить при линейном преобразовании исходной системы уравнений путем замены переменных, т.е. переходя к другой системе координат при условии инвариантности мощности.
Рассмотрим преобразование системы координат ![]() и
и ![]() к системе координат, вращающихся в
пространстве со скоростью
к системе координат, вращающихся в
пространстве со скоростью ![]() (рис.10.2)
(рис.10.2)

Рис. 10.2
Введем новые оси ![]() вращающиеся со скоростью
вращающиеся со скоростью ![]() . Под вектором Х можем
подразумевать любую координату системы: ток, потокосцепление и т.п.
. Под вектором Х можем
подразумевать любую координату системы: ток, потокосцепление и т.п.
Формулы преобразования координат:
1. для варианта
заданных величин в осях ![]() и
и
![]()
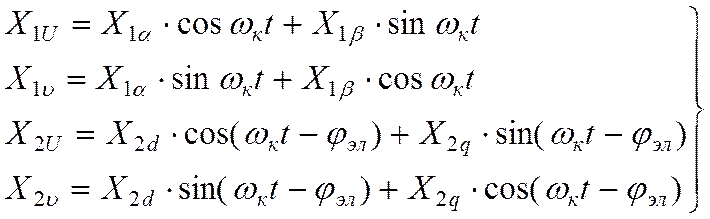 (10.7)
(10.7)
2. для обратного перехода
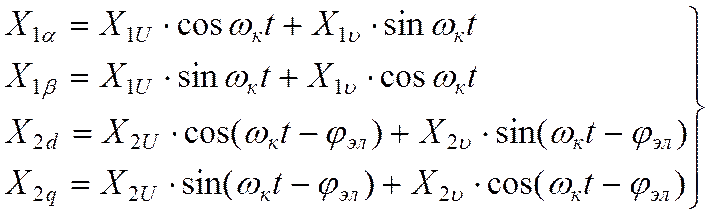 (10.8)
(10.8)
Подставив,
например, вместо Х величину 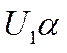 ,
получим
,
получим
![]()
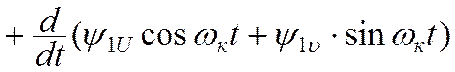 (10.9)
(10.9)
Это выражение соответствует уравнению:
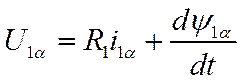 (10.10)
(10.10)
Аналогично получим выражения для ![]()
Путем различных преобразований можно получить
математическое описание обобщенной электрической машины 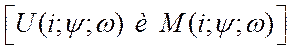 в
осях
в
осях ![]() .
.
Рассмотрим
различные варианты значений ![]() .
.
Вариант
![]() . Этот вариант позволяет привести реальные
переменные ротора, выраженные в осях
. Этот вариант позволяет привести реальные
переменные ротора, выраженные в осях ![]() к неподвижным осям
к неподвижным осям 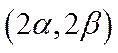 связанным со статором машины.
связанным со статором машины.
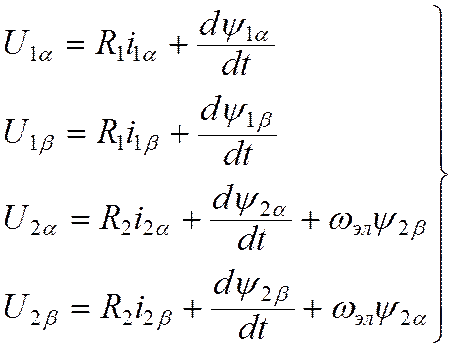 (10.11.)
(10.11.)
Вариант 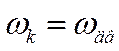 . Соответствует преобразованию реальных
переменных к осям
. Соответствует преобразованию реальных
переменных к осям ![]() , жестко связанным с ротором
машины.
, жестко связанным с ротором
машины.
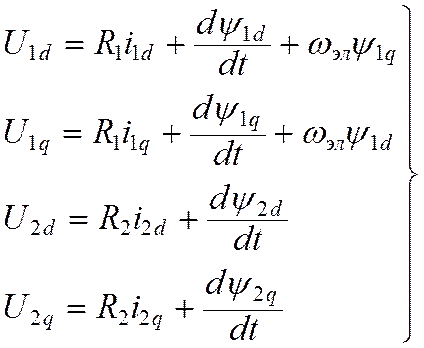 (10.12.)
(10.12.)
11. ЧТУ синхронным двигателем
Уточним некоторые особенности частотно – токового управления.
Рассмотрение на
уровне принципа действия позволяет утверждать, что для создания момента
постоянной величины (рамка с током в магнитном поле) угол между векторами тока
и потокосцепления (обобщенная эл. машина, §. 1.1) должен быть постоянным, т.е.
положение этих векторов должно изменяться в пространстве с одинаковой
скоростью. 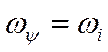
В общем случае, таким образом, управлять параметрами механической энергии на валу двигателя можно с помощью четырех воздействий: модуль потокосцепления, модуль тока, взаимная ориентация потокосцепления и тока и общая скорость вращения их векторов.
Схема частотно – токового управления для СД поясняется рис.11.1

Рис. 11.1
Вал бесконтактного
датчика углового положения (СС) связан с валом синхронного двигателя (СД).
Напряжения от датчика поступают через фазовые дискриминаторы в качестве заданий
на регуляторы токов фаз – три напряжения, свободные от несущей частоты ![]() и представляющие собой трехфазную систему
частоты вращения
и представляющие собой трехфазную систему
частоты вращения ![]() . Регуляторы охвачены сильной
обратной связью по току.
. Регуляторы охвачены сильной
обратной связью по току.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.