Автоматическое управление техническими системами. Система «Управляемый преобразователь – машина постоянного тока» как объект управления. Автоматическое регулирование координат электропривода. Частотно токовое управление АД, страница 4

2.1. МПТ при регулировании изменением подводимого к якорю напряжения.

Двигатель с независимым возбуждением – наиболее распространенный тип ДПТ. Рассмотрим его математическое описание. Будем считать, что размагничивающее действие реакции якоря скомпенсировано, а индуктивность якорной цепи постоянна. Полагая неизменными магнитный поток (f = const) и статический момент (M_c = const), можем принять.

При анализе динамики ЭП с ДПТ НВ можно ограничиться при принятых допущениях двумя уравнениями – уравнением равновесия ЭДС в цепи якоря и уравнением движения.

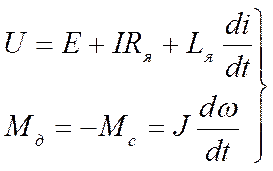                                                                              (2.1)

Указанные уравнения, естественно, далеки от полного описания привода. В реальных системах существуют дополнительные связи, обусловленные реакцией якоря, токами коммутируемых секций, падением напряжения под щетками и т.п. Однако заметного влияния на поведение системы они не оказывают и линиализированная система уравнений (2.1.) вполне пригодна для практического использования в подавляющем большинстве случаев.

Перепишем (2.1.) в более удобной форме

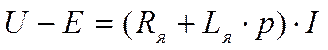                                                                        (2.2)

и

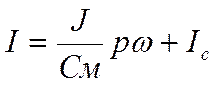                                                                                         (2.3)

из (2.2.) следует

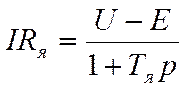                                                                             (2.4)

где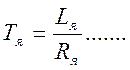

Следовательно, если на входе схемы имеем дифференциальное звено, оценивающее разность между напряжением и э.д.с. двигателя, то после инерционного (апериодического) звена с постоянной времени Т_я получим падение напряжения в цепи якоря. Вычитая из него падение напряжения, определяемое током статической нагрузки, согласно (2.3.) будем иметь

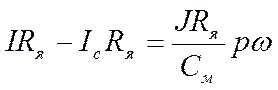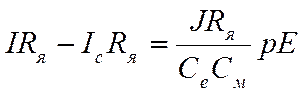                      , или       (2.5)

здесь 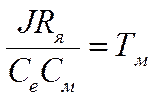– электростатическая постоянная времени.

Далее получаем

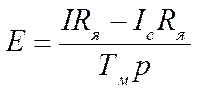                                                                                   (2.6)

Таким образом, на выходе интегрирующего звена с передаточным коэффициентом  получаем значение ЭДС двигателя, которое можно

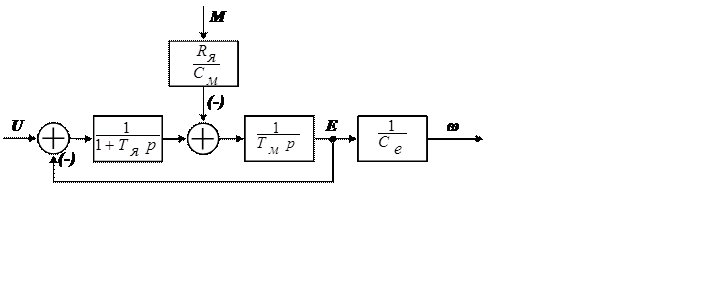
Рис. 2.1 Структурная схема ДПТ НВ в системе стабилизации скорости.

подать на вход системы. В итоге получаем структурную схему ДПТ независимого возбуждения (Рис. 2.1.)

Так как на выходе системы должна быть скорость вращения двигателя, то последовательно включаем безынерционное звено с передаточным коэффициентом. Возмущающее воздействие М_с также введено через безынерционное звено с коэффициентом R_я/С_м, на выходе которого имеем падение напряжения, обусловленного током  Ic.

Структурная схема Рис.2.1. может использоваться при исследовании электромеханических систем, предназначенных для управления скоростью.

В следящих системах на выходе имеем угол поворота исполнительной оси механизма j_м, который со скоростью двигателя связан соотношением

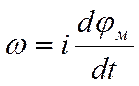                                                                                                     (2.7.)

где i – передаточное отношение редуктора.

Отсюда 

                                                                

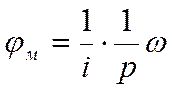
Следовательно, для следящего привода структурная схема должна быть дополнена ещё одним интегратором с передаточным коэффициентом  (Рис. 2.2.)

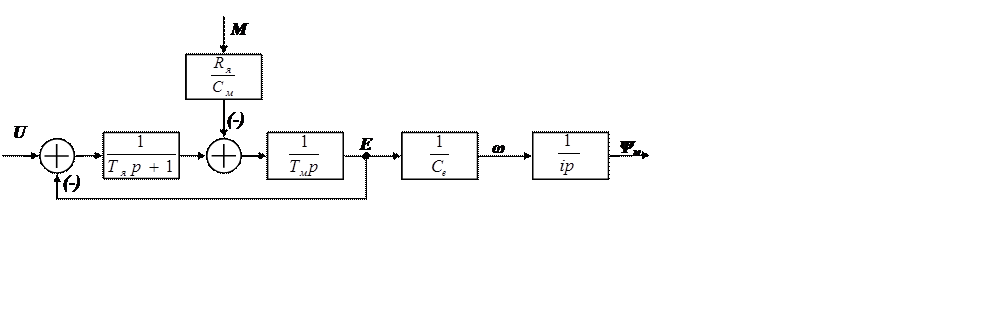
Рис.2.2 Структурная схема ДПТ НВ в следящем приводе.

По полученным структурным схемам можно записать передаточные функции для ДПТ НВ для режима управления скоростью двигателя:

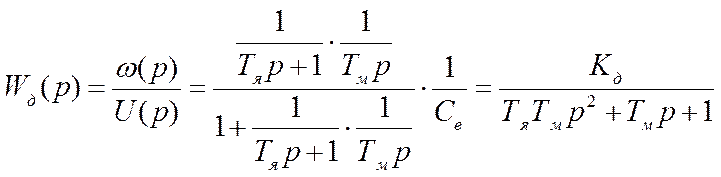                    (2.8)

Где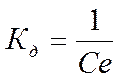; при управлении скоростью вращения рабочего органа – механизма вместо К_д вводится 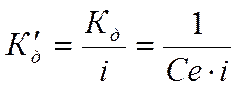 (2.9.)

Для следящего и позиционного привода:

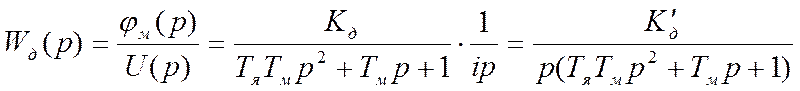         (2.10.)

При исследовании динамики ЭМС иногда пренебрегают электромагнитной постоянной, которая, как правило, значительно меньше электромеханической . В этом случае для системы управления скоростью

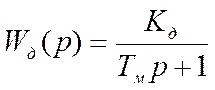                                                                                          (2.11.)

Для следящей и позиционной системы

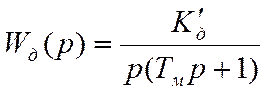                                                                                     (2.12.)