Автоматическое управление техническими системами. Система «Управляемый преобразователь – машина постоянного тока» как объект управления. Автоматическое регулирование координат электропривода. Частотно токовое управление АД, страница 14

                                                         

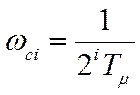
Когда требуется более высокая точность регулирования, при том же подходе применяют стандартную настройку на симметричный оптимум. При такой настройке желаемую передаточную функцию разомкнутого контура регулирования записывают в виде.

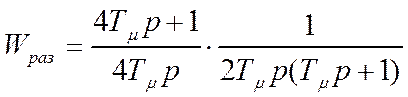                                                                      (4.29)

Формула (4.29) записана для первого контура. Для следующих контуров необходимо подставить. Здесь как и ранее предполагается, что все некомпенсированные инерционности исходного объекта  заключены в первом, внутреннем контуре.

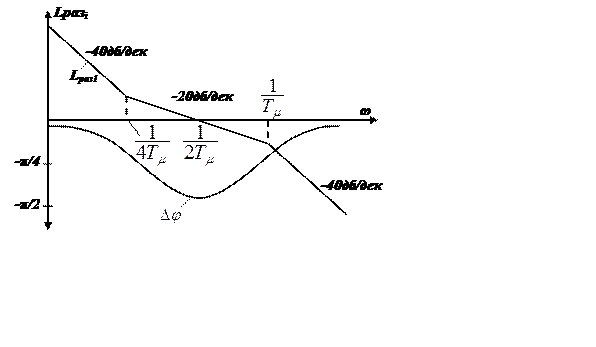
Рис. 4.8

Частотные характеристики, соответствующие (4.29) представлены на Рис. 4.8.

Разомкнутый контур при этом обладает астатизмом второго порядка, что увеличивает точность регулирования, особенно в процессах, близких к статическим. Вместе с тем наличие протяженного участка в низкочастотной области с наклоном -40 дб/дек уменьшает запас по фазе на частоте среза и увеличивает перерегулирование, которое может достигать 56%, что во многих случаях не приемлемо.

Сравнивая настройки на технический и симметричный оптимум, отметим,  что при средних и высоких частотах их ЛАЧХ практически совпадают. Следовательно, быстродействие и затухание колебаний в системе при этих двух стандартных настройках примерно одинаковы.

4.5. Синтез СПР.

Рассмотрим последовательность синтеза системы стабилизации скорости ДПТ независимого возбуждения при питании (забегая несколько вперёд) от тиристорного преобразователя. На Рис.4.9. приведена структурная схема разомкнутой системы.

Рис. 4.9 структурная схема разомкнутой системы.

На Рис. 4.10. схема замкнутой системы с регуляторами тока и скорости.

В первую очередь синтезируем регулятор тока. Исходная передаточная функция контура тока в соответствии со схемой имеет вид:

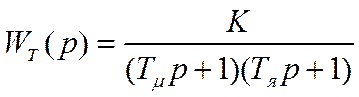                                                              (4.30)

где к – передаточный коэффициент звена.

Желаемая результирующая передаточная функция при включении регулятора тока должна иметь вид:

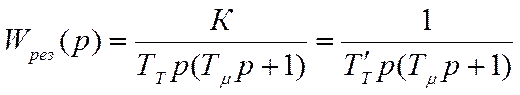              (4.31)            

где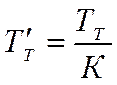

Отсюда передаточная функция самого регулятора

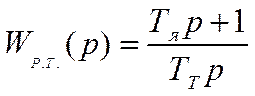                                                                           (4.32)

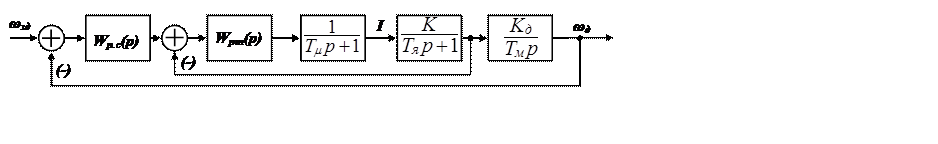
Рис. 4.10 Структурная схема замкнутой системы с регуляторами тока и скорости.

Для обеспечения динамических свойств с учётом настройки на технический оптимум примем.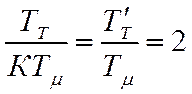

Тогда

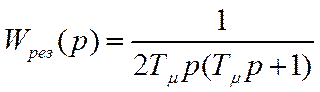                                                                                (4.33)

После замыкания контура тока получим:

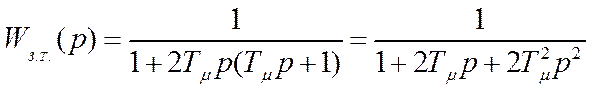                                          (4.34)

или, пренебрегая членом, в который входит квадрат малой постоянной ,

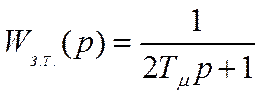                                                                                        (4.35.)

Для контура скорости в разомкнутом состоянии до введения регулятора имеем:

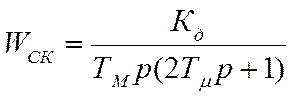                                                                                   (4.36)

где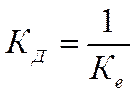

Теперь  представляет собой малую некомпенсируемую постоянную времени контура скорости.

После введения регулятора необходимо получить:

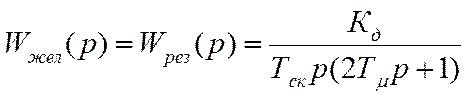                                                            (4.37)

где .

Отсюда сам регулятор должен иметь передаточную функцию:

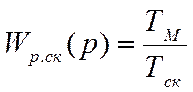                                                                                                   (4.38)

т.е. в этом случае регулятор будет пропорциональным.

Приняв  получим:

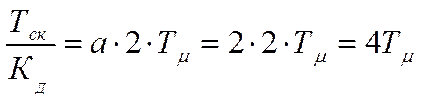                                                                 (4.39.)

или

                                                    

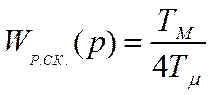
Следовательно

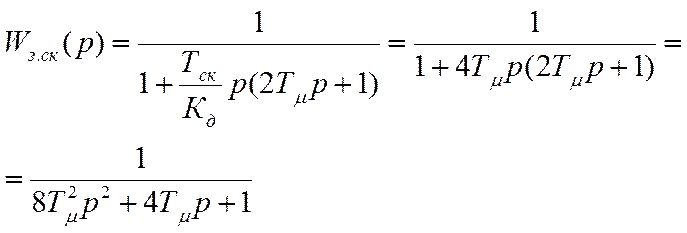                            (4.40.)

Характеристическое уравнение при этом:

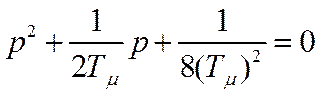                                                                                 (4.41.)

Отсюда для всей системы имеем:

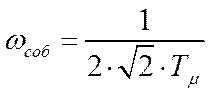
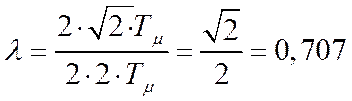
При этом, как отмечалось ранее, перерегулирование составит   σ ≈ 5%

Рассмотрим синтез следящей системы, в котором третьим контуром будет являться контур положения (Рис. 4.11).

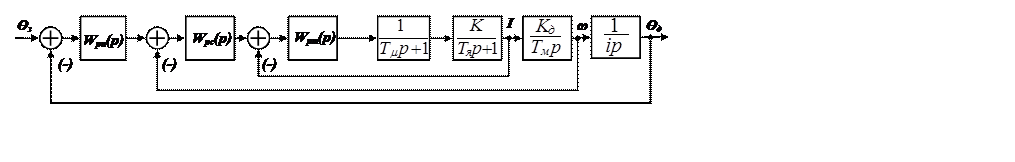
Рис. 4.11