Автоматическое управление техническими системами. Система «Управляемый преобразователь – машина постоянного тока» как объект управления. Автоматическое регулирование координат электропривода. Частотно токовое управление АД, страница 37

В современной практике используются преобразователи частоты трех видов: с промежуточным звеном постоянного тока и автономным инвертором тока или напряжения (ПЧ-АИ) (рис.8.4а), непосредственные (НПЧ) (рис.8.4б) и с широтно –импульсной модуляцией (ПЧ-ШИМ) (рис.8.4в) выпрямленного напряжения.

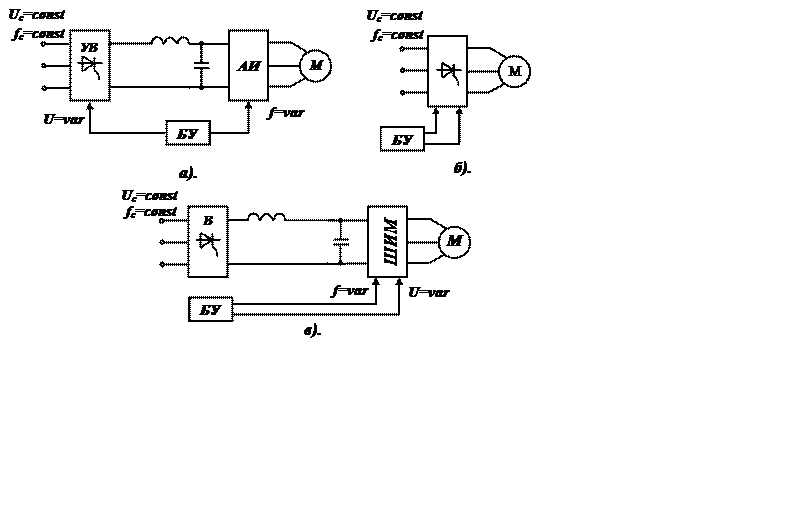
Рис. 8.4

В преобразователях на рис.8.4а и 8.4в частота регулируемого напряжения не ограничивается, в НПЧ диапазона регулирования частоты ограничен 3-20 Гц при частоте в сети 50 Гц. В преобразователях с ШИМ существенно лучше остальных гармонический состав токов.

Наиболее простым способом исследования механических характеристик системы ПЧ-АД является способ с использованием схемы замещения.

Эквивалентная схема замещения фазы привода ПЧ-АД при соединении обмоток статора  и ротора в звезду и приведенных активных и реактивных составляющих сопротивлений ПЧ к цепи статора приведена на рис.8.5

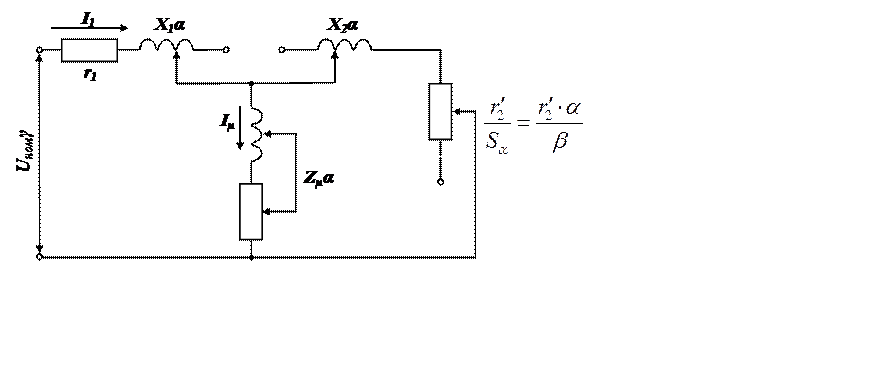
Рис. 8.5

Здесь неизменным остается только эквивалентное активное сопротивление статорной цепи привода . Индуктивные составляющие сопротивлений пропорциональны относительному значению частоты питания :

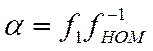                                                                                                         (8.7)

     При расчетах используются абсолютное отклонение угловой скорости  ,  относительное  и абсолютное  скольжение ротора:

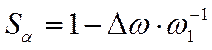                ;   ;                 (8.8)

где  - частота вращения магнитного поля при частоте тока в статоре  и  соответственно;  -  частота вращения ротора.

При составлении схемы замещения использованы следующие допущения:

· Выходное напряжение преобразователя (напряжение питания двигателя) принято синусоидальным и равным:

                                                                         

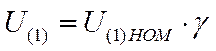
где  - относительное значение напряжения первой гармоники питания двигателя.

· Параметры   и  считаются постоянными, т.е. не зависящими от нагрева машины, не зависит от частоты и вытеснения тока в роторе, а насыщение не влияет на  и.

·  Не учитывается падение напряжения в статоре от тока намагничивания.

·  Проводимость намагничивающего контура не зависит от нагрузки.

·  Не учитываются добавочные потери в машине, обусловленные потерями на трение и в стали.

·  Не учитываются вибрационные и демпфирующие (паразитные) моменты, создаваемые взаимодействием высших гармонических МДС и токов двигателя.

С учетом вышеизложенного, выражение для механической характеристики имеет вид:

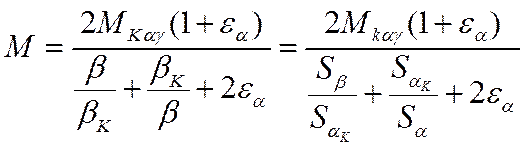                                             (8.9)

Здесь максимальное значение момента:

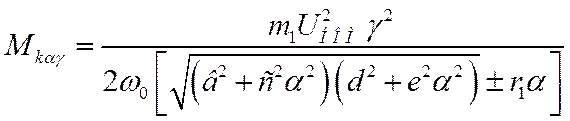                                     (8.10)

где + для двигательного режима, - для генераторного.

Максимума момент достигает при абсолютном скольжении:

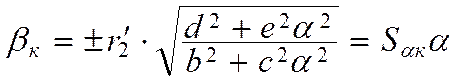                                                     (8.11)

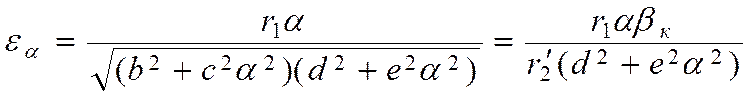                 (8.12)

где    ;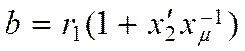

;       

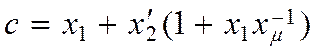
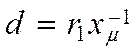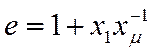
8.3. Законы оптимального управления системой ПЧ-АД

Значение зависит от частоты и амплитуды питающего напряжения. Наличие двух независимых каналов управления при частотном регулировании позволяет реализовать в системах ПЧ-АД оптимальное управление. Закон такого управления установил М. П. Костенко:

Если при регулировании скорости перегрузочная способность двигателя 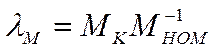 остается постоянной, можно записать, пренебрегая активным падением напряжения в обмотке статора:

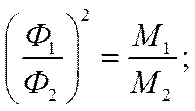
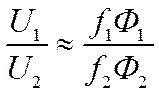                                                                   (8.13)

Следовательно,

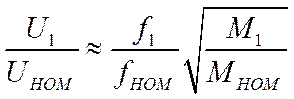                              или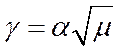                        (8.14)

Выражение (8.14) – математическая формулировка оптимального закона частотного управления при . Управляя движением по этому закону при ненасыщенной магнитной системе можно сохранить практически неизменным  и  - абсолютное скольжение, а КПД независимым от изменения скорости.

Виды нагрузки определяют различные формы взаимосвязанного статического управления напряжением и частотой.

При постоянном моменте нагрузки:

  или                                                                        (8.15)

При постоянной мощности

                                                                                                        (8.16)