Паровые турбины. Газотурбинные установки. Двигатели внутреннего сгорания, страница 21

Таким образом, при максимально возможной высоте лопатки (определяемой механической прочностью) p_i при нормальной скорости пара через последнюю ступень может быть пропущено только определенное количество пара. При заданных начальных и конечных параметрах пара развиваемая турбиной мощность пропорциональна проходящему через нее количеству пара, которое будет ограничиваться пропускной способностью последней ступени. Мощность, развиваемая при этих условиях, называется предельной.

1.23. Понятие о коэффициенте возврата тепла паровой турбины

Отношение полезно использованного теплоперепада в ступени к располагаемому теплоперепаду есть внутренний относительный КПД ступени.

            ,                                                                (1.80)

где ξ – относительные потери соответствующего вида, ξ = ∆ h_пот/∆ h_т.

Внутренний относительный КПД ступени меньше, чем КПД ступени, определяемый по формуле (1.80), и его максимальное значение приходится на менее выгодное отношение u/с₁.

В многоступенчатой турбине внутренние потери в отдельной ступени приводят к некоторому росту энтальпии пара на выходе из ступени (рис 1.22) и одновременно к увеличению располагаемого теплоперепада последующей ступени из–за расхождения изобар (∆h_2–3 < ∆h'_2–3).

В результате сумма располагаемых теплоперепадов всех ступеней оказывается больше располагаемого теплоперепада по изотропе .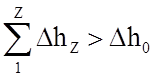

Или, иначе,

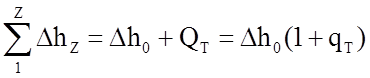                                          , (1.81)

где q_T  = Q_T / ∆h₀ называют коэффициентом возврата теплоты, который характеризует долю внутренних потерь, используемых в последующих ступенях турбины. Обычно q_T = 0,04 ÷ 0,1, что является существенным преимуществом многоступенчатой турбины перед одноступенчатой.

Коэффициент возврата тепла можно определить по приближенной формуле

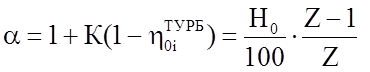                                          . (1.82)

где К – коэффициент, зависящий от вида пара. Например, при перегретом пара К = 0,2; при влажном – К = 0,12.

1.24. Понятие о характеристическом коэффициенте паровой турбины

Как уже было отмечено, КПД отдельной ступени в большой степени зависит от отношения u/с₁ (заметим, что для турбин со ступенями скорости наивыгоднейшее значение отношения будет: u/с₁ = cos α₁/2z, где z  – число венцов рабочих лопаток на ободе диска).

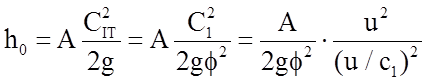                                     ,                                                                (1.83)

откуда можно получить

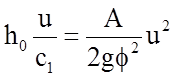                                                        .               (1.84)

Просуммировав левую часть уравнения (1.84), получим:

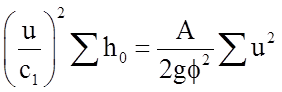                                                ,        (1.85)

Из последнего равенства имеем:

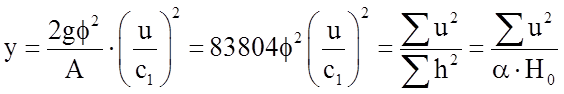                         .                                                                (1.86)

Выражение (1.86) представляет собой характеристический коэффициент паровой турбины (коэффициент Парсонса), где α – коэффициент возврата теплоты.

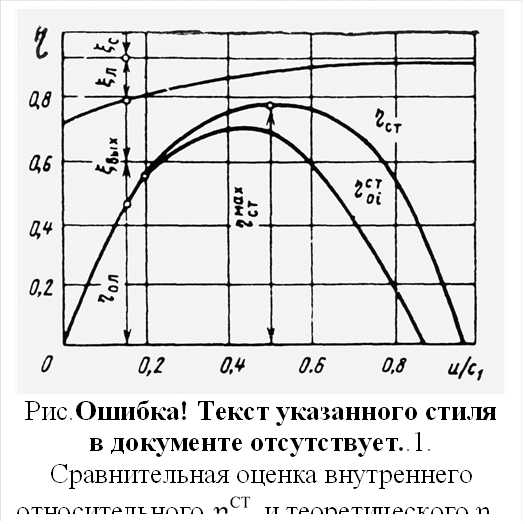
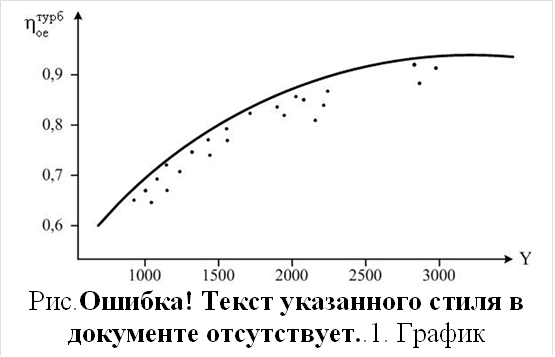
Коэффициент y позволяет оценить экономичность турбины в целом. Значение относительного эффективного КПД турбины связано с значением y следующим графиком (рис. 1.23), полученный опытным путем.

Из графика видно, что величина КПД пропорциональна y. Вплоть до значения y = 2000 КПД турбины быстро растет, а при y > 3000 значение КПД даже уменьшается.

1.25. Удельные единичные мощности паровых турбин

Применительно к паровым турбинам используют понятие внутренние мощности, развиваемые соответственно реальной турбиной:

                                                           ,                  (1.87)

где D, ∆h₁ – расход пара через турбину, располагаемый теплоперепад;

Идеальной турбиной (без внутренних потерь):

                                                          .                  (1.88)

Эффективная мощность (мощность на валу), обозначаемая N_е, которая связана с внутренней (индикаторной) через значение механического КПД турбины, учитывающего механические потери:

                                                          .                 (1.89)

Для современных турбин η_мех = 0,99 – 0,995.