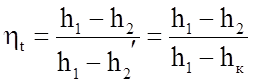Паровые турбины. Газотурбинные установки. Двигатели внутреннего сгорания, страница 12

                                                  .          (1.14)

Рис. 1.8. Процесс адиабатного расширения пара в системе h-s	Рис.1.9. Дополнительный график рис 1.8

В действительности в тепловых двигателях расширение пара происходит не по адиабате, а по политропе.

Процесс адиабатного расширения пара в системе h-s, откуда получим: h₀ = h₁ – h₂.

На пересечении изобара Р₁ и изотермы t₁ находим точку 5 (состояние пара перед входом в турбину). Таким образом, определена энтальпия пара в точке 5, т. е. h₁.

Из точки 5 проводим вертикаль (адиабату) до пересечения в точке 6 с изобарой Р₂ и находим энтальпию пара в точке G.

Величину t_к можно учитывать, если на продолжении изобара р₂ дойти до ее пересечения с верхней пограничной кривой (точка а – см. дополнительный график).

Из диаграммы s–h верно, что чем ниже р_2, тем меньше t_к и, следовательно, тем больше η_t цикла.

Уравнение (1.13) можно переписать и так:

                                             .     (1.15)

Разность энтальпий ∆h_t называют располагаемым теплоперепадом.

Удельный расход пара будет:

                                                            .                   (1.16)

Работу паровых машин оценивают по двум факторам:

– экономичности, которая характеризуется долей тепла, превращенного в механическую работу из всего количества тепла, затраченного на производство пара. КПД полезного действия, характеризующие экономичность паровой турбины, называются абсолютными;

– степень совершенства двигателя, определяемой сравнением его с идеальным двигателем. Тогда КПД, характеризующие совершенство машины, называют относительными.

По диаграмме h-s находят располагаемый теплоперепад ∆h_t , т. е. как разность энтальпий (теплосодержаний) при начальных и конечных параметрах пара. Действительный процесс расширения пара на диаграмме h-s изображается политропой, а такая разность энтальпий будет характеризовать количество тепла, превращение в механическую энергию в действительном двигателе, работающем с потерями тепла.

Тогда относительный внутренний КПД учитывает внутренние потери турбины в целом и определяется отношением:

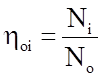                                                             ,                    (1.17)

где N_i = Д·∆ h_i – внутренняя (индикаторная) мощность, развиваемая реальной турбиной;

      Д – расход пара через турбину (допускается, что Д = const);

      N_o = Д·∆ h_o – внутренняя (идеальная) мощность, развиваемая идеальной турбиной, работающей без внутренних потерь.

Значение внутреннего относительного КПД ступени будет:

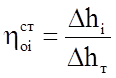                                                            .                   (1.18)

где ∆h_i – полезно используемы теплоперепад ступени;

      ∆h_т – располагаемый теплоперепад.

Механический КПД оценивает механические потери турбины:

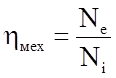                                                            ,                   (1.19)

где N_е – эффективная мощность (на валу), которая меньше внутренней (индикаторной) N_i мощности на величину мощности механических потерь

Для современных турбин η_oi = 0,7 – 0,88; η_мех = 0,99 – 0,995.

1.10. Суживающееся сопло с косым срезом

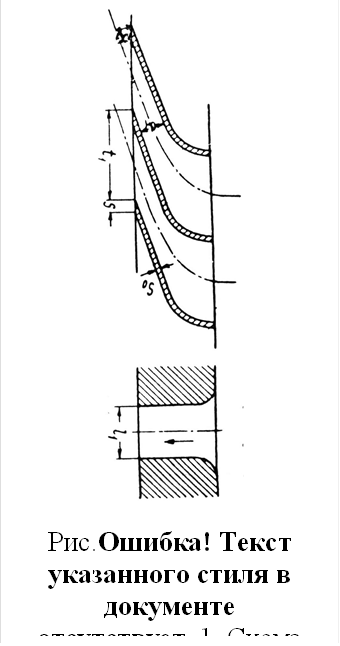Для подвода пара к рабочим лопаткам, сопла располагают под некоторым углом к плоскости вращения лопаток. Поэтому в выходной части сопла образуется косой срез (рис 1.10).

Из термодинамики известно, что простые суживающиеся сопла способны превращать в кинетическую энергию ограниченный перепад давлений, а именно от Р₀ до давления в минимальном сечении Р_крит, которое называют критическим b_крит.

Отношение давлений тогда можно записать так:

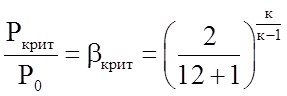                      .              (1.20)

Процесс расширения пара в суживающемся сопле с косым срезом при условии 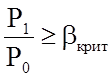 протекает так же, как и в простом прямом сопле. Если же 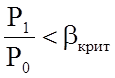, то в косом срезе сопла пар дополнительно расширяется сверх значения (Р₀ – Р_крит) с известным увеличением скорости истечения выше критической и повышением угла наклона струи при входе на рабочие лопатки по сравнению с углом наклона самого сопла.