Паровые турбины. Газотурбинные установки. Двигатели внутреннего сгорания, страница 13

В формуле (1.20) показатель адиабаты К возрастает с увеличением температуры перегретого пара и уменьшается с повышением его давления. Среднее значение К для перегретого пара принимают равным 1,3. Тогда по (20) β_крит = 0,546.

Для сухого пара К = 1,135, а при давлениях более 30 ата К берут более 1,135. При К = 1,135 – β_крит = 0,577.

Показатель К для влажного пара меньше, чем для сухого. Величина К зависит от степени сухости, начального давления и перепада давлений.

Более точно значении К рассчитывают по формуле:

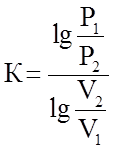                                                            .                    (1.21)

Критическая скорость для суживающегося сопла:

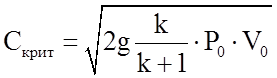                                                 .        (1.22)

Для перегретого пара при К = 1,3:

                                                    .            (1.23)

Для сухого пара при К = 1,135:

                                                    .            (1.24)

Более просто и точно критическая скорость определяется с помощью h–s диаграммы:

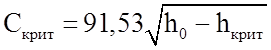                                                 .        (1.25)

Если процесс истечения идет через суживающиеся сопла, а отношение <β_крит, то струя пара в минимальном сечении имеет давление Р_крит>Р₁. Поэтому по выходе из сопла струя разрывается избытком внутреннего давления (Р_крит – Р₁); возникают завихрения, но существенного увеличения скорости не происходит.

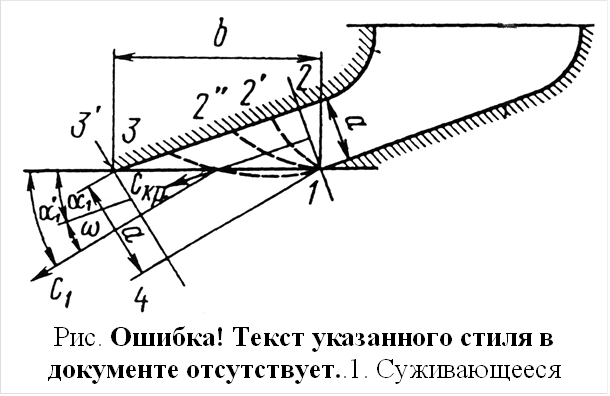
Таким образом, применять суживающиеся сопла для сверхкритических перепадов давлений нецелесообразно. На рис 1.11 показано суживающееся сопло с косым срезом, где нанесены расчетные размеры такого сопла.

1.11. Расширяющееся сопло с косым срезом

При рассмотрении движения струи в сопловых и лопаточных решетках, тепловой процесс считают установившимся. Следовательно, полагают, что параметры струи в любой точке межлопаточного канала со временем не меняются, а скорость в комплектах лопаток – для всех точек одного и того же сечения канала скорость струи пара одинакова (условно полагают).

Явления при движении струи весьма сложны и до конца не изучены. Поэтому газодинамическую теорию приходится дополнять опытными коэффициентами, что позволяет проводить расчеты приемлемые для практики.

Теоретическая скорость сечения может быть найдена в зависимости от интервала давлений по известной из термодинамики формуле:

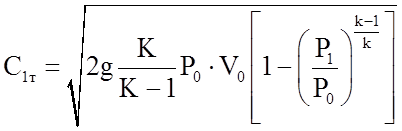                                        ,                                                                (1.26)

где P₀, V₀, P₁, k – параметры пара перед истечением, за соплом, показатель адиабаты.

Теоретический расход пара определяют по уравнению неразрывности струи:

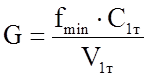                                                          ,                 (1.27)

где f_min, V_1т – площадь минимального сечения сопла, удельный объем при выходе струи (по конечному давлению Р₁)_.

После преобразований формул (1.26) и (1.27), получим выражение для плотности потока или весовой скорости, кг/м²·с:

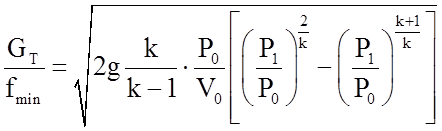                                     ,                                                                (1.28)

Полное превращение в кинетическую энергию струи с любым перепадом давлений и энтальпий достигается применением расширяющихся сопел Лаваля. При достаточной длине расширяющейся части давление постепенно снижается от критического в минимальном сечении до давления окружающей среды Р₁.

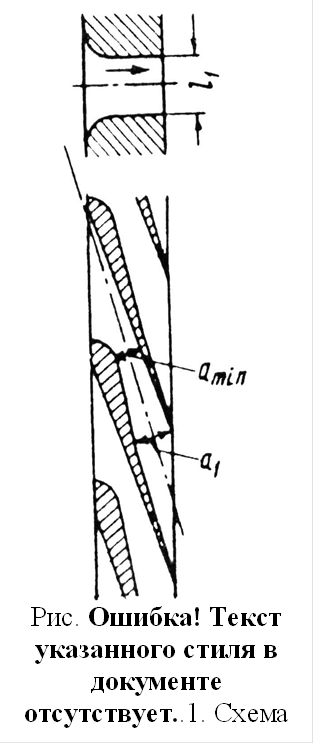
За счет дополнительного падения давления в расширяющейся части сопла Лаваля от сечения а_min до сечения а₁, энтальпия h уменьшается, и скорость увеличивается до величины, значительно превышающей критическую С >> С_крит.

Расход пара через сопло Лаваля равен расходу через суживающееся сопло одинакового минимального сечения.

В сопле с косым срезом (рис 1.12) происходит процесс, аналогичный протекающему в расширяющейся части сопла Лаваля.

Однако расширение в косом срезе отличается от расширения в сопле Лаваля. Дело в том, что при достаточной длине расширяющейся части сопла Лаваля можно превратит в кинетическую энергию любую разность давлений, а сопло с косым срезом способно использовать только ограниченный
интервал давлений.