Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 9

                         связей в  i-м  единичном состоянии ( от Х_i = 1 );

                C_S   – жёсткость сечения стержня при деформации, соот-

                         ветствующей усилию S ;

                 C_j   – жёсткость j-й упругой связи;

                e_S,t  – свободные (нестеснённые)  температурные дефор-

                         мации, соответствующие силовым факторам S ;

                D_(j) – компоненты заданных смещений связей..

25

         В  подынтегральных  выражениях  формул ( 1.11 )  и  ( 1.12 ) усилия, характеристики сечений и температурные деформации – функции от координаты x_j в локальной собственной системе координат j-го участка ( или элемента ), начало  которой  совпада-ет с одним из концов участка, а осью абсцисс является продоль-ная ось стержня^*):   S_i = S_i (x_j),   S_k = S_k (x_j),   S_F = S_F (x_j),   C_S = C_S (x_j),   e_S,t = e_S,t (x_j).

         Для плоской стержневой системы:

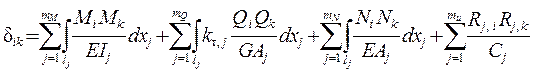 ;  ( 1.13 )

Dtnr, j

Dt2, j

– кри-

( 1.14 )

 

 

Dt0, j

Dt1, j

h2 j

визна  и относительная продольная

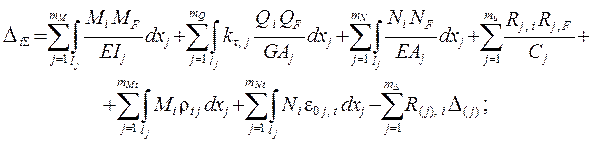
деформация  оси  стержня  от изме-

h1 j

менения  температуры  ( рис. 1.10 ); 

Dt_{nr, j}  и Dt_{0, j}– неравномерная и рав-

номерная  составляющие прираще-

ний температуры  j-го  участка;

h _j – высота сечения;

a_j – коэффициент линейного темпе-    

ратурного  расширения  (КЛТР).                      Рис. 1.10

^*)  В случае криволинейного стержня вместо декартовой координаты x_j  

     используется криволинейная координата s_j .

27

         Вычисленные коэффициенты и свободные члены канони-ческих уравнений должны быть проверены, для чего исполь-зуются суммарные единичные силовые факторы – внутренние усилия S_s в так называемом суммарном единичном состоянии основной  системы  ( от одновременного действия  всех основных неизвестных,  равных единице: неизвестныхнейная координатао декартовой координаты   X₁ = 1, …, X_n = 1 ),  а  также  возни-

кающие в этом состоянии реакции упругих связей R_{j, s} ()

и реакции R_{(j), s} связей с заданными смещениями D_(j) ():

         1) собственное обобщённое суммарное единичное переме-щение d_ss по направлениям всех удалённых лишних связей, вычисляемое по формуле

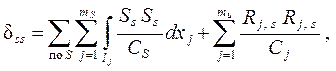                                       ( 1.15 )

должно   быть   равно   сумме   всех   коэффициентов  КУМС   ( это универсальная проверка коэффициентов ):

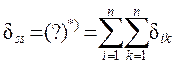                                    ;                           ( 1.16 )

         2) суммарное единичное перемещение по направлению i-й удалённой лишней связи

                                            ( 1.17 )

должно  быть  равно  сумме  коэффициентов  i-го канонического уравнения ( это  построчная  проверка  коэффициентов,  произво-димая при невыполнении условия ( 1.16 ) ):

28

                                                                        ( 1.18 )

         3) обобщённое ( суммарное ) перемещение D_sS  по  направле-ниям всех удалённых лишних связей от заданных воздействий, вычисляемое по формуле

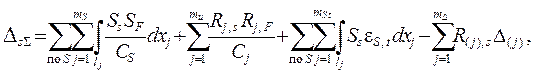 ( 1.19 )

должно быть равно сумме всех свободных членов КУМС:

*)  Символ (?) здесь и далее указывает на необходимость проверять      выполнение записанного условия.

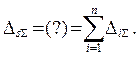                                                                      ( 1.20 )

27

         Для плоской системы зависимости ( 1.15 ) – ( 1.20 ) прини-мают вид