Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 17

           Для симметричных систем выбор групповых неизвестных может выполняться по имеющему чёткий смысл критерию: новые неизвестные должны быть группами реакций удалённых лишних связей, обладающими свойствами прямой или обратной симметрии.  Алгоритм действий при этом таков:

– выбирается^*) симметричная основная система путём удаления лишних  связей  в  симметрично  расположенных  точках  ( сечени-ях ),  в том числе на оси симметрии ;

– вместо  выявленных  основных неизвестных  X₁, X₂, … , X_nвво-

дятся новые ( групповые ) неизвестные каждое из

которых представляет собой либо симметричную, либо обратно-симметричную группу реакций удалённых лишних связей.

^*)  Из возможных симметричных вариантов.

С

а)

         Самый простой приём получения групповых неизвестных – парная группировка:  реакции  X_i  и  X_k

двух удалённых лишних связей в сим-

Xi

Xk

метрично расположенных точках  ( се-

б)

чениях )  заменяются  двумя  группами

силовых факторов того же типа, что и

исходные X_i  и  X_k – сил или моментов

a

a

и( рис. 1.12 ). При этом сама ос-

новная система не изменяется.

         Условие статической эквивален-                Рис. 1.12

тности   исходных  и  новых  неизвест-

ных:  или

         Полученные  и – соответственно симметричная и обратносимметричная^*)   группы   реакций   удалённых  лишних

Номера

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

связей. Матрица преобразования

неизвестных .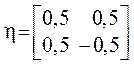

         Номера исходных и группо-  h =   0 0… 0,5 0…0  0,5  0…0

вых неизвестных могут не совпа-           . . . . . . . . . . . . . . . . . . . .

дать, тогда фрагмент общей ( для           0 0… 0,5 0…0 –0,5 0…0

Номера Х

всей системы ) матрицы h  имеет            . . . . . . . . . . . . . . . . . . . .

вид, показанный на рис. 1.13.                             i               k            

         Замечание:  исходные неиз-                        Рис. 1.13

вестные в точках (сечениях), рас-

положенных на линии симметрии, сами по себе являются сим-метричными или обратносимметричными и поэтому не требуют группировки.

         На рис. 1.14 приведён пример выбора групповых неизвест-ных метода сил. При построении основной системы ( рис. 1.14, б ) из методических соображений проигнорирована рекомендация 2 ( см. с. 9 ) о нежелательности удаления линейных связей.

         Исходные и групповые неизвестные связаны следующими зависимостями:

 ( устанавливаются простым сопостав-

лением  рис. 1.14, б  и  1.14, в ).   Реакции Х₃ и Х₄  внутренних свя-                            

ричная».

^*)  Используются также термины «антисимметричная» и «кососиммет-

зей в шарнире, расположенном на оси симметрии, сами по себе являющиеся групповыми ( Х₃ – симметричная, Х₄ – обратносим-метричная ),  при  переходе  к  новым  неизвестным  остаются  без изменений.  На  рис. 1.14, г  –  матрица  преобразования  неизвест-

ных h.  – симметричные основные неизвестные,

X4

С

 – обратносимметричные.