Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 3

e

h

P

G

B

A

 а)                                                      б)       

 

A

                                                                                                         

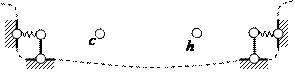                                                                        в)                          

Рис. 1.1

         Для  фермы  (рис. 1.1, б)  по  формуле ( 1.3 ): Y = 6  ( включая опорные узлы); С = 9; С₀ = 4; n_st = – Применяя выра-жение ( 1.2 ), имеем K = 8 ( AdcA, cdehc, cdec, dehd, BheB, AchBA и два контура у опор А и В,  образованные «землёй»  и опорными стержнями ); Н = 22;  n_st =  Если шарнирные опоры А и В

представить иначе, применив к упругим связям гипотезу отвер-дения (рис. 1.1, в), то исчезают два приопорных контура и шесть шарниров опорных связей, тогда K = 6; Н = 16;  n_st =

7

1.2. Идея метода сил

         Сутьидеи:  если  основные  неизвестные  ( реакции  лишних связей )  найдены,  то  любые  силовые  факторы  в  системе  далее могут быть определены из условий равновесия её частей или узлов.

         Так как для определения силовых факторов в СНС недо-статочно одних лишь уравнений статики, то для отыскания ос-новных неизвестных используются дополнительные зависимо-сти, являющиеся, согласно принципу двойственности в механике, кинематическими  ( описывающими  геометрическую сторону за-дачи ). Их количество равно числу лишних связей ( ровно столь-ко, сколько недостаёт уравнений равновесия ); их смысл – равен-ство перемещений по направлениям лишних связей при одина-ковых ( заданных ) воздействиях в двух системах – рассчитывае-мой статически неопределимой ( РСНС ) и системе, полученной из исходной СНС удалением лишних связей с приложением вза-мен них реакций ( она называется основной системой метода сил – ОСМС). Выполнение указанных кинематических условий обес-печивает эквивалентность деформированных, а следовательно, и напряжённых состояний РСНС и ОСМС. Будучи выражены на основании физических соотношений через силовые факторы, в том  числе  основные  неизвестные  метода  сил  ( реакции  лишних связей ),  геометрические  ( кинематические )  уравнения  позволя-ют найти эти неизвестные.

9

1.3. Основная система метода сил

       Основная система метода сил – это геометрически неизменяемая и, как правило, статически определимая систе-ма, получаемая из рассчитываемой СНС путём удаления лишних связей с приложением вместо них реакций этих связей.

         При изображении основной системы реакции удалённых лишних связей ( основные неизвестные метода сил ) обозначают-ся, независимо от их типа (силы или моменты), как X₁ , X₂ , …, X_n . 

         Данное выше определение основной системы допускает возможность удаления как всех, так и части лишних связей. В первом случае число основных неизвестных n совпадает со сте-пенью  статической  неопределимости n_st ,  и  получаемая  ОСМС статически определима. Во втором случае n < n_st , и основная си-стема остаётся статически неопределимой. Но если для неё воз-можен расчёт по вспомогательным формулам или табличным данным, её использование может быть целесообразным.

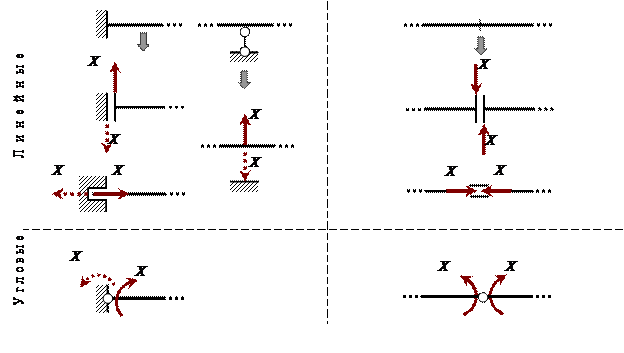
         На рис. 1.2 показано, как изображаются на схеме основной системы неизвестные Х – реакции различных удаляемых лишних связей – внешних и внутренних, линейных и угловых.

                          У  д  а  л  я  е  м  ы  е       с  в  я  з  и

               в  н  е  ш  н  и  е                           в н у т р е н н и е