Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 11

51

49

         Кинематическая( деформационная )проверка – вычисление перемещений, которые в заданной системе заведомо равны нулю ( по направлениям жёстких связей ).

52

         В методе сил главной является кинематическая проверка, так как с её помощью контролируется выполнение исходного требования кинематической эквивалентности ОСМС и рассчи-тываемой системы ( см. с. 6 и 11 ), а именно – обеспечения равен-ства нулю полных перемещений в ОСМС по направлениям уда-лённых лишних связей при значениях неизвестных Х и соответ-ствующих им усилий S, найденных в результате расчёта .

         Кинематическая проверка выполняется путём вычисления указанных перемещений по формулам метода Максвелла–Мора с использованием для определения упругих деформаций основ-ной системы найденных усилий S. Контролируемыми перемеще-ниями могут быть:

         1) обобщённое ( суммарное ) перемещение D_s  по  направле-ниям всех удалённых лишних связей,  вычисляемое  по  формуле

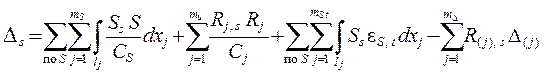 ( 1.27 )

( здесь S_s , R_{j, s} и R_{(j), s} – суммарные единичные усилия  и  реакции ); оно должно быть равно нулю – этот контроль результатов назы-вается их  универсальной ( полной ) кинематической проверкой ;

          2) перемещение D_i по направлению некоторой i-й удалён-ной лишней связи

, ( 1.28 )

которое тоже должно быть равным нулю –частная кинематиче-ская проверка. В ( 1.28 ) S_i , R_{j, i} и R_{(j), i} – усилия и реакции от X_i = 1.

         Последние  два  слагаемых  в  формуле  ( 1.28 )  требуют  вы-полнения в точности тех же самых вычислений, с помощью ко-торых при температурных и кинематических воздействиях опре-деляются свободные члены канонических уравнений. Так как их повторение не имеет смысла, то вычисляется только часть пере-мещения D_i ,  обусловленная  упругими  деформациями  ОСМС  –

 ( с удержанием первых двух членов в ( 1.28 )). Результат дол-жен быть равен  – ( D_it + D_ic ).

         При расчёте «вручную» кинематическая проверка произво-дится путём «перемножения» эпюр найденных усилий S (для плоских стержневых систем – M , Q и N )  с  одноимёнными  еди-ничными ( M_i , Q_i , N_iили суммарными M_s , Q_s , N_s ) по следующим формулам:  

              = (?) = – ( D_st + D_sc ) =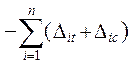              ( 1.29 )       

                  ( универсальная кинематическая проверка );

        

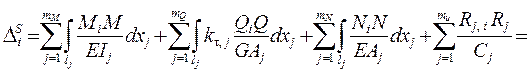
                                         = (?) = – ( D_it + D_ic )                              ( 1.30 )       

                         ( частная кинематическая проверка ). 

          В случае заданных  силовых  воздействий ( нагрузок ) D_it = 0

и D_iс = 0, поэтому результаты вычислений  и  по формулам

( 1.29 ) и  ( 1.30 ) должны быть равными нулю ( с допустимыми погрешностями счёта ),  если  усилия  M , Q  и  N  найдены  верно. При заданном изменении температуры  расчёт  по ( 1.30 )  должен дать значение перемещения, совпадающее со взятым с противо-положным  знаком  ранее  вычисленным  свободным  членом  i-го  канонического  уравнения,  а   по  ( 1.29 ) –  с  суммой  всех  свобод-ных  членов  ( температурных  перемещений  в  ОСМС ). Проверка результатов  расчёта  на  смещения  связей  заключается  в  сопо-

бодными    членами   Diс   канонических   уравнений   и  их  суммой ( также  с  противоположным знаками ).

ставлении итогов вычислений  и  по ( 1.29 ) и ( 1.30 ) со сво-

         Замечания: 1) при выполнении кинематической проверки необходимо учитывать те же виды деформаций элементов, что и при определении коэффициентов и свободных членов КУМС;

2)  кинематическая проверка  может давать  положительный результат  даже при непра-

вильных  единичных  усилияхS_i  и  S_s  ( не  удовлетворяющих  уравнениям статики ).

1.6.  Матричная форма расчёта статически

неопределимых систем методом сил