|
|
||||||||
|
|
||||||||
![]()
![]()
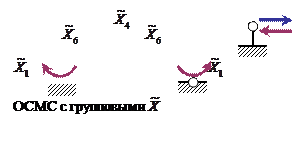 |
|||
|
|||
![]()
|
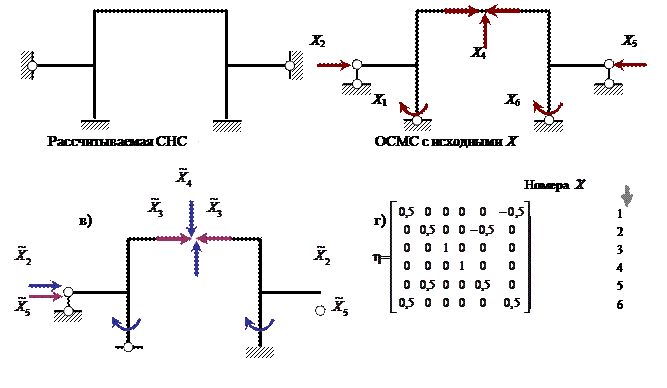
Рис. 1.14
Канонические уравнения метода сил для определения групповых неизвестных – такие же по форме и общему смыслу, как при использовании «естественных» неизвестных:
![]() , ( 1.38 )
, ( 1.38 )
но их коэффициентами и свободными членами являются переме-
щения ![]() в
основной системе МС по направле-
в
основной системе МС по направле-
ниям групповых неизвестных, т. е. обобщённые ( групповые ) пе-ремещения, представляющие собой комбинации линейных и угловых перемещений симметрично расположенных точек ( сечений ).
Объединение всех симметричных групповых неизвестных в вектор ![]() , а обратносимметричных – в вектор
, а обратносимметричных – в вектор ![]() позволя-ет матричные уравнения ( 1.38 )
представить в виде
позволя-ет матричные уравнения ( 1.38 )
представить в виде
![]()
![]()
![]()
![]()
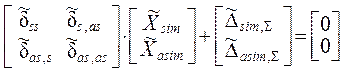 , ( 1.39 )
, ( 1.39 )
где ![]() – матрица
собственных единичных перемещений
в ОСМС
– матрица
собственных единичных перемещений
в ОСМС
по направлениям симметричных неизвестных ![]() ( от
( от
![]() =
1 );
=
1 );
![]() – матрица перемещений в ОСМС по направлениям сим-
– матрица перемещений в ОСМС по направлениям сим-
метричных неизвестных ![]() от единичных
обратно-
от единичных
обратно-
симметричных![]() = 1;
= 1;
![]() – матрица перемещений в ОСМС по
направлениям обрат-
– матрица перемещений в ОСМС по
направлениям обрат-
носимметричных неизвестных ![]() от
единичных сим-
от
единичных сим-
метричных![]() = 1;
= 1;
![]() – матрица
собственных единичных перемещений
в ОСМС
– матрица
собственных единичных перемещений
в ОСМС
по направлениям симметричных
неизвестных ![]() ( от
( от
![]() = 1 );
= 1 );
![]() и
и ![]() – перемещения в ОСМС от заданных воздействий
– перемещения в ОСМС от заданных воздействий
по направлениям ![]() и
и ![]() соответственно.
соответственно.
Все вышеперечисленные перемещения определяются мето-дом Максвелла – Мора с
использованием симметричных и обрат-носимметричных единичных эпюр ![]() и
и ![]() .
.
|
![]()
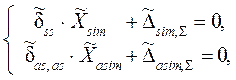 ( 1.40 )
( 1.40 )
|
|
обратносимметричных воздействиях составляются и решаются только
уравнения второй подсистемы с обратносимметричными ![]() .
.
Проверки результатов расчёта выполняются по правилам,
изложенным в п. 1.5, с использованием в соответствующих формулах единичных
усилий ![]() и
и ![]() .
.
По найденным групповым
неизвестным![]() при необходи-мости могут быть вычислены
исходные:
при необходи-мости могут быть вычислены
исходные: ![]() .
.
![]()
|
основан на том, что симметричные или обратносимметричные воздействия вызывают в заданной СНС только деформации и перемещения соответствующего типа, что позволяет рассмат-ривать и рассчитывать половину системы, расположенную по одну сторону от оси симметрии, так как в другой половине перемещении, деформации и силовые факторы такие же (при симметричном воздействии), как в рассчитываемой половине, или отличаются от них только знаком в случае обратносиммет-ричного воздействия*).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.