Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 24

моменты ),  входящие в интегралы формулы  ( 2.7 ),  и  реакции  смещаемых связей, с помощью которых вычисляется пере-мещение  .  Заметим,   что  если  бы  была  выбрана  консольная

ВСОС по

58

схеме рис. 2.4, в, то все единичные реакции смещае-мых связей оказались бы равными нулю, тогда = 0.

         Как и в случаях  двух других видов воздействий ( силовых и тепловых ), применение вспомогательной СОС в этой задаче ра-ционально,  если силовые факторы  S_c , R_{j, c}  и  R_{(j), c}  ранее  найдены     расчётом СНС на кинематическое воздействие.

60

2.4. Матричнаяформа определения перемещенийСНС

 Значения n перемещений в статически неопределимой си-стеме от v вариантов заданных комбинированных воздействий   ( с  силовыми,  тепловыми  и  кинематическими  составляющими ) можно записать в виде матрицы

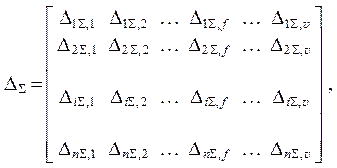                ( 2.8 )

где  f = 1, 2, …, v – номер варианта воздействий;

        i = 1, 2, …, n – номер искомого перемещения.

         Для  определения  этих  перемещений  методом  Максвелла – Мора служит матричная формула

             ( 2.9 )

где L , L_t и R_D – матрицы  усилий  в  упруго  деформируемых  эле-

                          ментах  и  связях,  на  участках  с  температурными

                          деформациями  и  реакции  смещаемых  связей   в

                          единичных  состояниях  заданной  статически  не-

                          определимой системы от фиктивных воздействий

                          F_iM_i = 1 ( i=)  по направлениям искомых пе-

                          ремещений;

           B  и  B_t – матрицы  внутренней  упругой   и   температурной

                          податливостей;

                   Е = diag [ 1 1 … 1 ];

                    S – матрица  внутренних  усилий  и  реакций  упругих

                          связей  в  статически  неопределимой  системе  от

                          заданных  воздействий  ( результаты  расчёта  СНС

                          по вариантам  f = 1, 2, …, v );  вместо Sможно ис-

                          пользовать S_F ( только от силовых воздействий );

            Т  и  D – матрицы   приращений   температур   и   заданных

                          смещений связей по вариантам воздействий.

         Объединение матриц, входящих в ( 2.9 ), даёт выражение

                          ( 2.10 )

где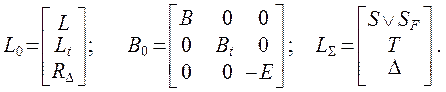

         Если матрицу L_S формировать в виде L_S = diag [ S  T  D ], то матрица искомых перемещений будет D_S = [ D_F  D_t  D_c ] – с разде-лением результатов по видам воздействий. 

         Приведём далее матричные формулы для вычисления пере-мещений отдельно от силовых, температурных и кинематичес-ких воздействий по всем изложенным выше вариантам, в том числе с использованием вспомогательных статически определи-мых систем ( матричные аналоги выражений ( 2.1 ) – ( 2.7 )):

– вариант а,           ( 2.11 ) – вариант б,           ( 2.12 ) – вариант в,           ( 2.13 )

                                  

– вариант а,           ( 2.14 ) – вариант б,           ( 2.15 )

                 

– вариант а,           ( 2.16 ) – вариант б,           ( 2.17 )

                  

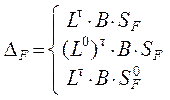
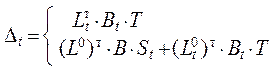
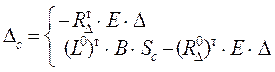
где L⁰,и– матрицы  усилий  в  упруго  деформируемых  эле-

                          ментах  и  связях,  на  участках  с  температурными

                          деформациями  и  реакции  смещаемых  связей   в

                          единичных состояниях вспомогательной статиче-

                          ски определимой системы  от  фиктивных  воздей-

                          ствий  F_iM_i  = 1 ( i=)  по направлениям иско-

                          мых перемещений;

      S_F , S_t  и S_c – матрицы  внутренних  усилий  и  реакций  упругих

                          связей  в  статически  неопределимой  системе  от

                          заданных  силовых,  температурных  и  кинемати-

                          ческих воздействий.