DS – матрица ( при одном варианте заданных воздействий –
вектор ) перемещений в ОСМС по направлениям удалён-
|
![]()
|
![]()
|
|
|
|||||
|
|||||
|
|||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а) б)
а) б)
 |
|||||||||
|
|||||||||
|
|||||||||
|
|
 |
|||
 |
|||
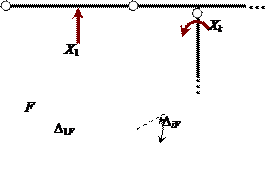
Рис. 1.9
В k - м единичном состоянии ОСМС ( рис. 1.9, в ) возникают перемещения d1k , d2k , …, dik , …, dkk , …, dnk , являющиеся компо-
нентами k-го столбца матрицы d.
![]()
|
и её компонентов:
|
( Det (d)![]() – это является достаточным
условием геометричес-
– это является достаточным
условием геометричес-
кой неизменяемости ОСМС ), положительно определённая
( Det (d) > 0 ), симметричная относительно главной диагонали;
2) главные коэффициенты – собственные перемещения dii ![]() – существенно положительные ( dii > 0 );
– существенно положительные ( dii > 0 );
![]()
|
|
|
и свободных членов КУМС, их проверки
Коэффициенты канонических уравнений ( единичные пере-мещения ![]() в ОСМС ) и их свободные члены ( пере-мещения DiS
в ОСМС ) и их свободные члены ( пере-мещения DiS ![]() от заданных воздействий ) определяются методом
Максвелла–Мора*) по формулам
от заданных воздействий ) определяются методом
Максвелла–Мора*) по формулам
|
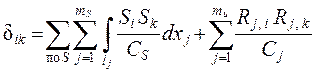 ; ( 1.11 )
; ( 1.11 )
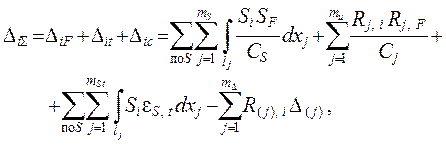 ( 1.12 )
( 1.12 )
где SF и Rj,F – внутренние силовые факторы ( в общем случае –
изгибающие и крутящие моменты, продольные и
поперечные силы ) и реакции упругих связей в ос-
новной системе от заданной нагрузки ( силового
воздействия );
![]() *) В частных случаях возможно использование других методов,
*) В частных случаях возможно использование других методов,
например, метода начальных параметров для балок.
Si, Rj, i и R(j), i – внутренние усилия, реакции упругих и смещаемых
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.