Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 12

         Матричная запись канонических уравнений метода сил имеет вид ( 1.7 ):                  

1.6.1. Основные матричные соотношения и формулы

26

          Матрица внешней упругой податливости основной систе-мы метода сил вычисляется по формуле

                                 ( 1.31 )

где L – матрица   усилий   в   упруго  деформируемых  элементах

             ОСМС ( в т. ч. упругих связях )  в  единичных состояниях:

38

                                     L = [ L₁ L₂ … L_i … L_n ];

      L_i – вектор усилий в i-м единичном состоянии ( от X_i = 1 );

             для плоской стержневой системы:

                 M_i   – вектор изгибающих моментов   в расчётных сече-

      L_i  =     Q_i   – вектор поперечных сил               ниях   расчётных

41

                N_i   – вектор продольных сил               участков^*) упруго

                R_{c, i}  – реакции упругих связей              деформируемых

единичном состо- янии ОСМС;

                                                                                                       стержней     в    i-м

                  M_{1, i}                 Q_{1, i}               N_{1, i}             

                    :                      :                     :                

       M_i =    M_{j, i}     ;  Q_i =   Q_{j, i}     ;  N_i =    N_{j, i}      ;  M_{j, i} – вектор изгиба-

                    :                      :                     :          ющих  моментов   в

                                              расчётных сечениях        

стка в i-ом единичном состоянии:

                                                                        j-го расчётного уча-

                 

с тремя расчёт-ными сечениями;

двумя расчётны-ми сечениями;

       M_{j, i} =    – для участка      M_{j, i} =              – для  участка  с

                 

       M_j,i =  – для участка с одним расчётным сечением;

^*)  Правила назначения расчётных участков и сечений изложены ниже.

                b_j , c_j , e_j – начало, середина и конец        b_j         c_j               e_j

lj / 2

lj / 2

                                 j-го  расчётного  участка;      

                  Q_{j, i} , N_{j, i}  – по структуре аналогичны

M_{j, i} ;                                                Рис. 1.11

          m_M , m_Q , m_N  – количества   расчётных  участков изгибающих

                                 моментов, поперечных  и  продольных сил со-

                                 ответственно;

41

R_c,i = [ R_{1, i} … R_{j, i} … R_{u, i} ]^т ;  u – число упругих связей;

        B=diag [B_MB_QB_N B_c ]  –  матрица    внутренней     упругой

                               податливости основной системы метода сил;

        B_M , B_Q , B_N  – матрицы   податливости   ОСМП   при   изгибе,

                               сдвиге и растяжении (сжатии) элементов соот-

                               ветственно;

39

        B_M = diag [……];

        – матрица податливости  j-го участка при изгибе;

                   в случае стержня постоянного сечения:

расчётными сечениями;

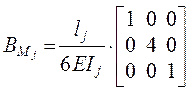                     – для участка с тремя

сечениями;

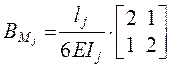                 – для участка с двумя расчётными

      = [ l_j / ( EI_j ) ] – для участка с одним сечением;

   B_Q ,B_N  – по структуре аналогичны B_M , с использованием вмес-