Xi ) от одновременного действия всех основных неизве-
стных X1, X2 , …, Xn – реакций удалённых лишних связей.
Также по принципу суперпозиции суммарное перемещение
|
, ( 1.7 )
где dik – перемещение в ОСМС по направлению i-й удалённой
лишней связи ( по направлению основного неизвестно-
го Xi ) от единичной реакции k-й удалённой лишней свя-
зи ( от Xk = 1 ).
1.4.2. Варианты записи и смысл канонических уравнений МС
Подстановка ( 1.6 ) и ( 1.7 ) в ( 1.5 ) дает систему уравнений
![]()
|
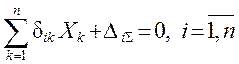 , ( 1.8
)
, ( 1.8
)
которые и называются каноническимиуравнениямиметодасил ( КУМС ).
Это неоднородные алгебраические уравнения, линейные относительно основных неизвестных Х.
В развёрнутом виде:
|
|
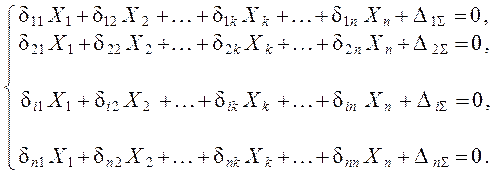 (
1.9 )
(
1.9 )
|
1. Система канонических уравнений в целом по сути – ки-нематические условия эквивалентности основной системы МС и заданной системы при одинаковых воздействиях и истинных реакциях Х удалённых лишних связей; по форме – отрицание полных перемещений в ОСМС по направлениям всех основных неизвестных Х.
2.
Произвольное ( i-е ) уравнение – отрицаниеполногопе-ремещения вОСМС по
направлению i-йудалённой лишней связи ( суммарного перемещения ![]() от заданных воздействий ( S ) и одновременно действующих реакций всех удалённых
лишних связей X1, X2 ,…, Xn ).
от заданных воздействий ( S ) и одновременно действующих реакций всех удалённых
лишних связей X1, X2 ,…, Xn ).
![]()
|
4. Свободный член i-го уравнения DiS – перемещениевОСМСпо направлениюi-йудалённойлишней связи ( по направ-лению основного неизвестного Xi ) от заданных воздействий (S).
5. Слагаемое dik Xk i-го уравнения – перемещениевОСМСпо направлениюi-йудалённойлишней связи ( по направлению основного неизвестного Xi ) от истиннойреакции Хkk-йуда-лённойлишней связи.
|
|
![]() По теореме Максвелла о взаимности единичных перемеще-ний dik = dki .
По теореме Максвелла о взаимности единичных перемеще-ний dik = dki .
|
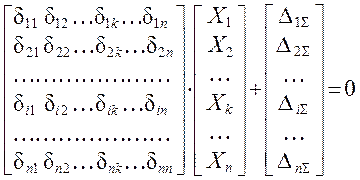 или
или ![]() (
1.10 )
(
1.10 )
![]()
![]()
![]() d X DS
d X DS
|
гой податливости основной системы МС по направлени-
ям основных неизвестных Х ;
Х – матрица ( при одном варианте заданных воздействий –
вектор ) основных неизвестных;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.