Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 19

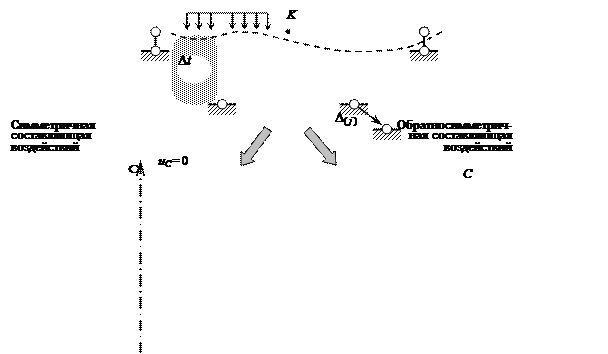
         Исходя из этого, заданные воздействия ( рис. 1.15, а ) пред-варительно  раскладываются  на  симметричную  ( рис. 1.15, б )  и обратносимметричную ( рис. 1.15, в ) составляющие. Затем на каждую из них выполняется расчёт половины системы, причём по двум разным схемам, с введением по оси симметрии связей, моделирующих влияние отбрасываемой второй половины при ограничениях на перемещения точек (сечений) заданной СНС, расположенных  на  оси  симметрии  ( C и K ),  в  двух  вариантах –при симметричных и обратносимметричных перемещениях. Эти кинематические условия с использованием горизонтальных u_C, u_K, вертикальных v_C, v_K перемещений и угла поворота q_K описа-ны на схемах деформаций, представленных на рис. 1.15, б, в.

 

^*)  Кроме деформаций сдвига и поперечных сил,  характер распределе-

    ния которых противоположен типу воздействия.

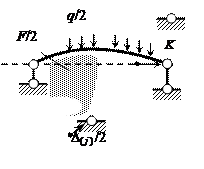
         Отвечающие им связи изображены на двух расчётных схе-мах левой половины СНС ( рис. 1.15, г, д ). Отметим, что сумма степеней статической неопределимости двух полученных рас-чётных моделей равна степени статической неопределимости за-данной СНС. Для рамы, изображенной на рис. 1.15, а, n_st = 5, полурама по рис. 1.15, г  имеет n_st = 3,  а система на рис. 1.15, д  дважды статически неопределима.

 

q

                                а)

 

vC = 0

          б)                                            в)

								C
						Dt /2
		Dt /2

 

          г)                                            д)

 

Рис.1.15

к ней линейные упругие связи.

         Замечание:  в случае, когда вдоль оси симметрии расположен прямолиней-ный стержень или упругая линейная связь, они условно «расщепляются» по продоль-ной оси и в рассчитываемой половине системы учитываются с половинной жёсткостью. Так  же  делятся  пополам угловые упругие связи на оси симметрии и перпендикулярные  

         Далее в обычном порядке выполняются два независимых расчёта по двум сформированным расчётным схемам. При этом суммарная трудоёмкость меньше, чем в прямом расчёте задан-ной симметричной СНС, даже если использовать в нём группи-ровку неизвестных. По полученным в двух расчётах результатам находятся искомые усилия от полных заданных воздействий – суммированием в пределах рассматриваемой половины и как разность для другой половины.

2. ПЕРЕМЕЩЕНИЯ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ

СИСТЕМАХ

         В инженерных расчётах строительных конструкций кроме усилий, необходимых для оценки прочности, требуется опреде-лять также характерные перемещения для проверки выполнения требований по жёсткости.

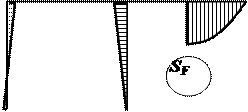
         Для вычисления перемещений в статически неопредели-мой стержневой системе в общем случае комбинации силовых, тепловых и кинематических воздействий ( на рис. 2.1, а   показано  действительное ( S ) состояние СНС ) можно использовать уни-версальную формулу Максвелла – Мора в форме ( 1.12 ) или ( 1.14 ) для плоских систем.  

а)                                                      б)

i

a'

 

         в)                                                     г)

 

Рис. 2.1