Основы теории расчёта статически неопределимых систем методом сил. Перемещения в статически неопределимых системах, страница 20

         Следует иметь в виду, что в рассматриваемой задаче о пе-ремещениях в СНС входящие в указанные формулы силовые факторы  S_F  и  R_{j, F} – это  внутренние  усилия  и  реакции  упругих связей в действительном состоянии рассчитываемой статичес-ки неопределимойсистемы от заданных нагрузок ( на рис. 2.1, в в качестве иллюстрации усилий S_F показана эпюра изгибающих моментов ).  ВместоS_F  и  R_{j, F}  могут  использоваться  суммарные силовые факторы  S_S  и  R_{j, S}  от всех воздействий,  включая темпе-ратурные  и  смещения связей  ( в главе 1  эти силовые факторы – результаты расчёта – обозначались S и R_j ),^*) – будет получено то же значение искомого перемещения.

         Иной смысл, чем в методе сил, имеют единичные усилия и реакции упругих связей S_i и R_{j, i} – они определяются в статиче-ски неопределимой системе от единичного воздействия – силы F_i = 1 или момента М_i = 1 по направлению подлежащего опреде-лению линейного или углового перемещения ( рис. 2.1, б, г ).

         Таким образом, для отыскания одного перемещения в СНС по общей формуле метода Максвелла – Мора необходимо выпол-нить расчёт СНС дважды – на заданные воздействия действи-тельного  состояния  ( S )  и  на  единичное  силовое  воздействие фиктивного  состояния  ( i ).  Вычисление  каждого  следующего перемещения требует нового расчёта СНС на соответствующую фиктивную единичную нагрузку. При компьютерном расчёте СНС в матричной форме эти фиктивные нагрузки рассматрива-ются как дополнительные варианты при формировании матри-цы L_S ( см. с. 26 ).

         «Перемножение» усилий S_F и S_i «вручную» при вычисле-нии интегралов в формуле Максвелла – Мора может быть трудо-ёмким из-за того, что от любого воздействия внутренние сило-вые факторы возникают, как правило, во всех элементах СНС.

         Если учесть особые свойства СНС и использовать в рас-чёте их перемещений вспомогательные статически определимые системы, то точные результаты могут быть получены значите-льно проще – объяснения и формулы даны ниже.

 

^*)  Необходимо  уяснить,  что  символы  и  обозначения  общей  теории

    определения перемещений не имеют никакого отношения к исполь-

    зуемым в методе сил «внутренним» одноимённым величинам.

2.1. Определение перемещений от силовых воздействий

         Альтернативными вышеупомянутому способу вычисления перемещений, который для случая силовых воздействий в плос-кой стержневой СНС даёт формулу

57

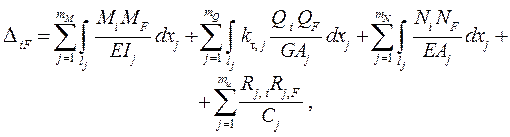        ( 2.1 )

являются выражения

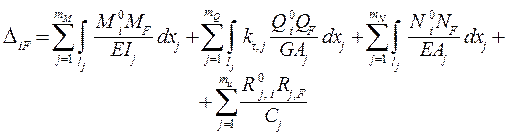         ( 2.2 )

и

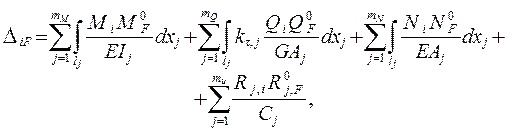         (2.3 )

где – внутренние   усилия   и   реакции   упругих

                                       связей   во  вспомогательной  статически

                                       определимой системе  от  единичного воз-

                                       действия F_i= 1 или М_i= 1 по  направлению

                                       искомого перемещения; 

    – внутренние   усилия   и   реакции   упругих

                                       связей   во  вспомогательной  статически

                                       определимой системе  от заданной нагруз-

58

                                       ки.

         Вариант ( 2.2 )  рационален,  если  вычисление  перемещений выполняется  после  расчёта  СНС на заданную нагрузку, когда уже найдены силовые факторы M_F , Q_F , N_F  и  R_{j, F} .

         Использование  формулы  ( 2.3 )  выгодно  в  тех  случаях,  ко-гда по каким-либо причинам усилия в рассматриваемой СНС от заданной нагрузки находить не требуется, а нужны только перемещения.

59

         Вспомогательная статически определимая система ( ВСОС ) получается из заданной СНС удалением лишних связей. При её выборе рекомендуется руководствоваться следующим:

         1) вспомогательная СОС должна быть такой, чтобы усилия в ней от единичного фиктивного воздействия ( в случае исполь-зования формулы ( 2.2 )) или от заданной нагрузки ( по варианту ( 2.3 )) возникали бы на минимально возможном числе участков;