В заключение отметим, что в качестве вспомогательной можно использовать не обязательно
статически определимую систему, но и любую систему, полученную из
рассчитываемой СНС удалением не всех, а части лишних связей. Но эта теорети-ческая
возможность не даёт практической выгоды в сравнении с применением ВСОС.
2.2. Перемещения от изменения температуры
Определение перемещений в плоских стержневых СНС от температурных (
тепловых
) воздействий возможно по одной из двух формул,
вытекающих из универсальной формулы Макс-велла
–
Мора:
( 2.4 )
( 2.5 )
где Mi , Ni – изгибающие моменты и продольные силы в фиктив-
ном единичном состоянии рассчитываемой стати-
чески неопределимой системы от единичного воз-
действия Fi=
1 или Мi= 1 по направлению
искомого
перемещения;
температурные деформации;
aj –
коэффициент ли-
нейного температурного
расширения материала;
|
|
–
условно свободные (
нестеснённые
)
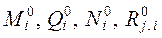– то же, что на с. 40;
Mt , Qt , Nt и Rj, t – внутренние усилия и реакции упругих свя-
зей в действительном состоянии рассчитываемой
статически неопределимой системы от заданного
изменения температуры, найденные в результате
расчёта
СНС;
– перемещение во вспомога-
тельнойСОС
от изменения температуры.
|
|
Рис. 2.4 является иллюстрацией к
определению перемеще-ний в СНС от изменений температуры двумя описанными выше
способами – по ( 2.4 ) и
( 2.5 ).
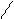
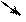
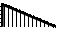
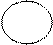
а)
б) в)
г)
д) е)
ж)
з) и)
Рис.2.4
В любом варианте предварительно вычисляются темпера-турные деформации rt и e0t для действительного состояния си-стемы ( рис. 2.4, а ).
В случае
использования формулы (
2.4
) расчётом заданной СНС на единичное воздействие (
рис. 2.4, б
) определяются уси-лия
Mi и
Ni (
рис. 2.4, д, з
), «перемножаемые» затем с
деформа-циями r
t и e
0t . При этом определять силовые факторы
Mtи
Nt в статически неопределимой раме не
требуется.
