Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 9

 Відповідь: .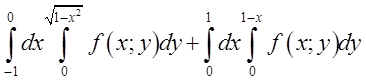

ПРИКЛАД 4.

 Обчислити інтеґрал Ейлера-Пуассона

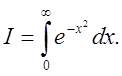
Розв'язання:

   Розв'язання .  Оскільки 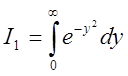   відрізняється від І лише формою запису змінної (замість х стоїть у)    то їх величини будуть однакові, а тому . Крім того  . А тому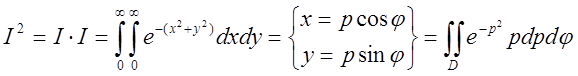

Обчислимо останній інтеґрал (рис. 4.9). Областю інтегрування є перший октант . В полярній системі цю область утворить промінь, який буде виходити з полюса, а тому , і прямуватиме в нескінченність, а тому . Це будуть межі внутрішнього інтегралу по . Починати свій рух промінь повинен з положення , а тому це буде нижня границя зовнішнього

Рис. 4.9                        інтегралу по , а закінчити свій рух промінь має в положенні 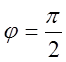, і це буде верхня границя зовнішнього інтегралу. Маємо 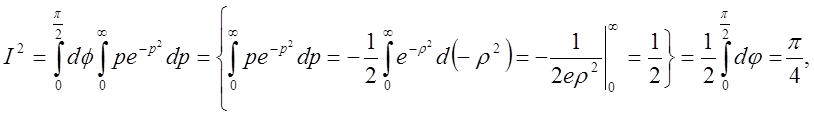 звідки  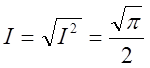тобто               

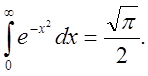
 Цей інтеґрал широко застосовується в теорії ймовірностей.

ПРИКЛАД 5.

Обчислити подвійний інтеграл ,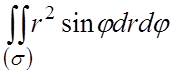

Розв'язання:

 Щоб визначити, як змінюється в області  полярний кут , проведемо проміні в точки А і В області .

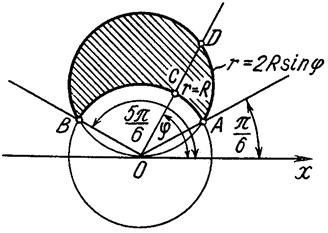
Розв’язуючи спільно рівняння ліній, обмежуючих область , знайдемо значення кута , відповідні променям ОА та ОВ: .

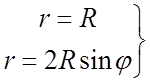Звідси .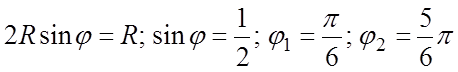

Таким чином, кут  в області  змінюється від  до .

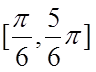          Тепер знайдемо границі зміни полярного радіуса в області . Під довільним кутом , взятому із проміжку , проведем із полюсу промінь OD. В точці С входу цього променя в область , а в точці D виходу його із області . Тому нижня та верхня границі у внутрішньому інтегралі дорівнюють відповідно  та .

.

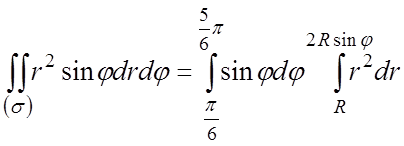(Ми винесли  за знак внутрішнього інтеграла, так як при обчисленні внутрішнього інтеграла змінна  зберігає постійне значення).

Внутрішній інтеграл

.

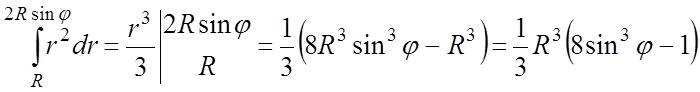Зовнішній інтеграл

.

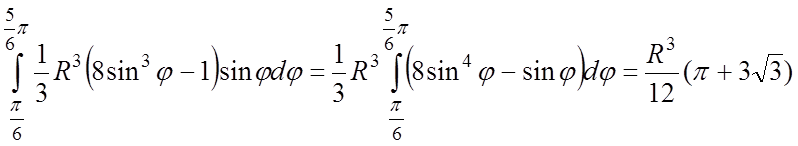2) Розв’язати самомтійно:

1.  Перемінити порядок інтегрування.

1.1. 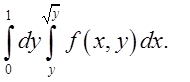 Відп.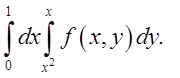

1.2. 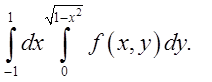 Відп.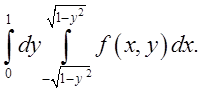

1.3.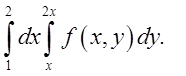Відп.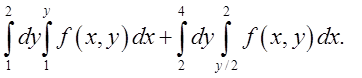

1.4.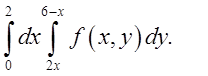Відп.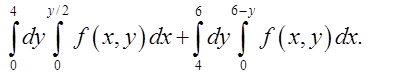

2.  Обчислити подвійні інтеграли у вказаних областях.

2.1.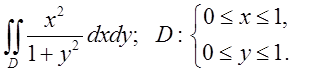 Відп.

2.2.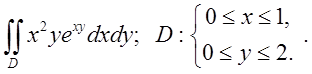Відп. 2.

2.3.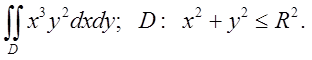Відп. 0.

2.4.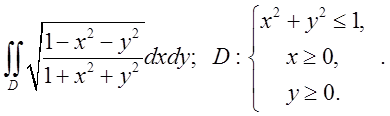Відп..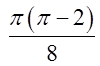

2.5.Відп.

Практичне заняття 8.

План:

8.1.Тема. Дослідження потрійних інтегралів, їх властивостей. Обчислення потрійних інтегралів. Заміна змінних.застосування в геометрії і фізиці.

8.2.Ціль:

1). Засвоїти потрійні інтеграли.

2). Властивості потрійного інтегралу.

3). Засвоїти заміну змінних у потрійному інтегралі.

8.3. Теоретичний матеріал подано в лекції номер 5.

8.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).

8.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 429-440.

8.6. На практичному занятті використовуються формули, таблиці, теореми.

          1). Обчислення потрійного інтегралу.

Потрійний інтеграл позначають так

 

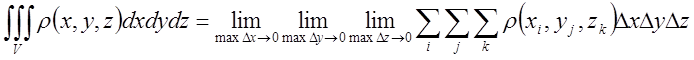
Маємо формулу для обчислення потрійного інтегралу:

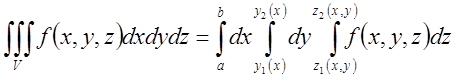
2). Властивості потрійного інтеграла аналогічні властивостям подвійного.

1) )                 

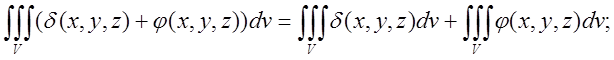
2)                                                          

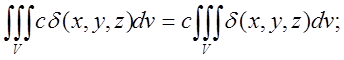
3) 

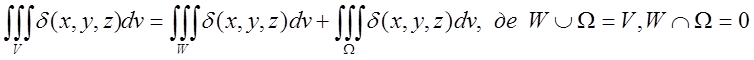
4)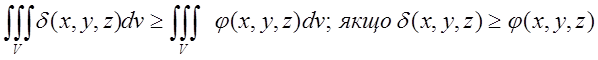5) 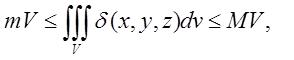 де  V – об’єм ,

6) Теорема про середнє значення: 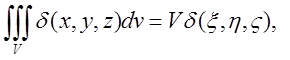де                                                                                        

         3). Заміна змінних у потрійному інтегралі.

Формула заміни змінних для сферичних координат має вид:

При   

         

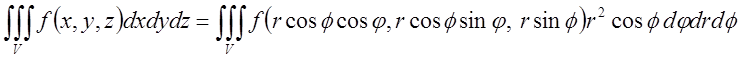
При

         

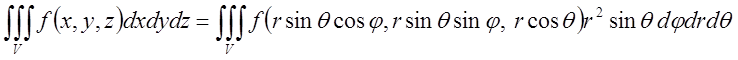
Формула заміни  прямокутних декартових координат на циліндричні в потрійному інтегралі має вид

         

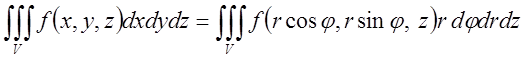
8.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

Оцінити  інтеграл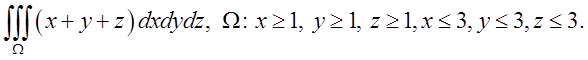

Розв’язок:

 Оцінювати будемо за 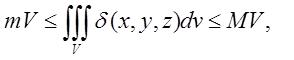 де  V – об’єм ,

 Обєм куба . Найменше значення підінтегральної функції в цьому кубові буде в точці (1,1,1) . Найбільше значення підінтегральної функції в цьому кубові буде в точці (3,3,3) , А тому

.

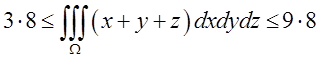ПРИКЛАД 2.

 Розставити границі інтегруваня  в  потрійному інегралі 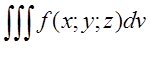   де    V-область обмежена площинами x+2y+3z=6 ;   x=0;  y=0; z=0;

Розв’язок: